Problema4: Cartas de Control

Ej4. La ausencia de imperfecciones (rayaduras, astillamientos, grietas, ampollas, etc) en los tableros de madera para uso en ebanistería, es una importante característica de calidad.

A fin de vigilar el proceso de fabricación, cada hora, durante 15 consecutivas, se selecciona un tablero acabado y se inspecciona para descubrir posibles imperfecciones. En la tabla que sigue, se registra el número de imperfecciones por tablero:

Tablero	Número de Defectos		Tablero	Número de Defectos
1	4		9	8
2	2		10	7
3	3		11	3
4	3		12	6
5	9		13	5
6	4		14	7
7	5		15	3
8	3

Determinar:

a) Los límites de control y la línea central de la carta C del número de defectos.

b) Traza la gráfica de control C, ¿se puede decir que el proceso está bajo control?.


Apartado a)

Realizamos una recopilación de los datos ofrecidos por el enunciado del problema:

· Carta de control C, número de defectos.
· Número de muestras: m = 15.

Nos piden obtener la carta de control del número de defectos, C, cuyos límites de control son:

Siendo:

·

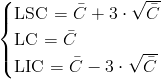
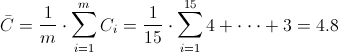
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de defectos, C:

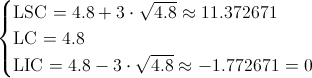
Observamos que el límite de control inferior es negativo, ésto es algo que no puede reflejarse en el estudio de cartas de control, por lo que lo igualamos a cero.


Apartado b)

Debemos representar la carta de control C, del número de defectos, pero antes, debemos obtener los límites σ y 2σ de la misma, para su posterior análisis mediante el método: Western Electric Handbook 1956.

Para obtener los límites de advertencia σ y 2σ, existen dos formas, una es mediante una simple regla de tres, y la otra, algo más sofisticada, es obteniendo el valor de σ.

En este caso, usaremos la regla de tres para obtener los límites de control de advertencia.

- Para el límite superior:

(LSC - LC)/3 = (11.372671 - 4.8)/3 ≈ 2.190890

Por lo tanto, los límites de advertencia de control 2σ son:

· c + 2·σ = 4.8 + 2·2.190890 = 9.18178

Para los límites de advertencia de control σ son:

· c + σ = 4.8 + 2.190890 = 6.99089

- Para el límite inferior:

(LC - LIC)/3 = (4.8 - 0)/3 = 1.6

Por lo tanto, los límites de advertencia de control 2σ son:

· c - 2·σ = 4.8 - 2·1.6 = 1.6

Para los límites de advertencia de control σ son:

· c - σ = 4.8 - 1.6 = 3.2

Podemos comprobar, que el límite superior y el inferior, el valor no es el mismo, esto es así ya que hemos tenido que adaptar el valor del límite de control inferior a cero, por darnos un valor negativo.

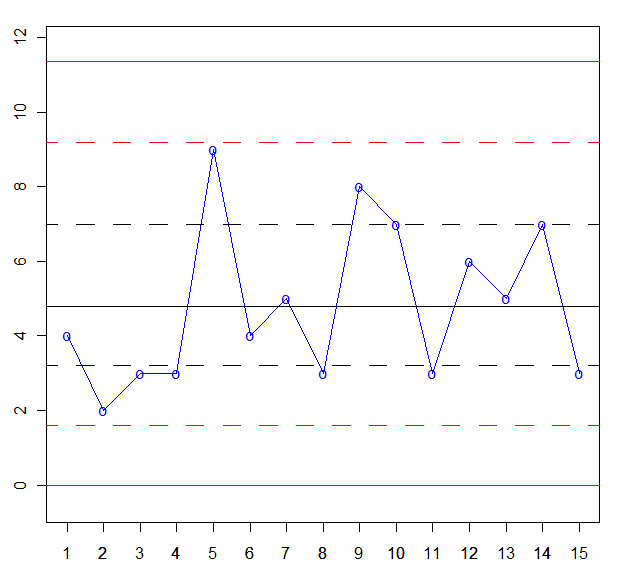
Y en este momento, estamos en disposición de realizar la gráfica de control C:

Una vez dibujada la gráfica de control, pasamos a su análisis. En un primer vistazo observamos que todos los puntos están dentro de los límites de control 3σ, pero el proceso está fuera de control porque 4 de 5 puntos consecutivos están a una distancia 1σ o superior de la línea central.

Los puntos son:

· 1: LC.
· 2: 1σ inferior.
· 3: 1σ inferior.
· 4: 1σ inferior
· 5: 1σ superior.

Por lo tanto, el proceso del número de defectos de la carta C, está fuera de control.