Problema33: Probabilidad

Ej33. Se selecciona al azar un alumno de cierta universidad y señalamos como A, el evento en que el individuo seleccionado tiene una tarjeta de crédito Visa y como B el evento análogo para una MasterCard.

Supongamos que P(A) = 0.5, P(B) = 0.4 y P(A ∩ B) = 0.25. Determinar:

a) Calcule la probabilidad de que el individuo seleccionado tenga al menos una de las dos tarjetas.

b) ¿Cuál es la probabilidad de que el individuo seleccionado no tenga ninguna de esas tarjetas?

c) Describa, en términos de A y B, el evento en que el alumno seleccionado tenga una tarjeta Visa, pero no una MasterCard, y a continuación calcule la probabilidad del evento.


Realizamos una recopilación dados por el enunciado del problema:

· Evento A ≡ 'Individuo que posee tarjeta de crédito Visa'.
· Evento B ≡ 'Individuo que posee tarjeta de crédito MasterCard'.
· Probabilidad A: P(A) = 0.5.
· Probabilidad B: P(B) = 0.4.
· Probabilidad A intersección B: P(A ∩ B) = 0.25.

Y empezamos a resolver los distintos apartados.


Apartado a)

En este apartado nos piden obtener la probabilidad de que al menos algunos de los individuos seleccionados, tengan, al menos, una de las dos tarjetas.

Por definición:

P(A U B) = P(A) + P(B) - P(A ∩ B) = 0.5 + 0.4 - 0.25 = 0.65

Por lo tanto, la probabilidad de que un individuo de cierta universidad posea al menos una de las dos tarjetas es de 0.65.


Apartado b)

En este apartado, nos piden hallar la probabilidad de que el individuo elegido al azar, no posea ninguna de las dos tarjetas mencionadas.

Por definición:

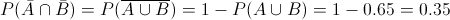
La probabilidad de que un individuo seleccionado al azar no posea ninguna de las tarjetas de crédito mencionadas es de 0.35.


Apartado c)

Por definición:

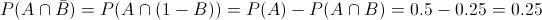
En definitiva, un individuo seleccionado al azar dada las condiciones del enunciado, la probabilidad de que posea la tarjeta Visa y no la MasterCard es de 0.25.