Problema8: Cartas de Control

Ej8. En la fabricación de placas de circuitos impresos, una característica de calidad importante es el espesor de la placa. En la tabla que sigue, se detallan, para 25 muestras de tamaño 3, estos espesores, en pulgadas, así como sus medidas muestrales:

Muestra	....X1..........X2...........X3	Media		Muestra	....X1..........X2...........X3	Media
1	0.0629......0.0636......0.0640	0.06350		14	0.0645......0.0640......0.0631	0.06387
2	0.0630......0.0631......0.0622	0.06277		15	0.0619......0.0644......0.0632	0.06317
3	0.0628......0.0631......0.0633	0.06307		16	0.0631......0.0627......0.0630	0.06293
4	0.0634......0.0630......0.0631	0.06317		17	0.0616......0.0623......0.0631	0.06233
5	0.0619......0.0628......0.0630	0.06257		18	0.0630......0.0630......0.0626	0.06287
6	0.0613......0.0629......0.0634	0.06253		19	0.0636......0.0631......0.0629	0.06320
7	0.0630......0.0639......0.0625	0.06313		20	0.0640......0.0635......0.0629	0.06347
8	0.0628......0.0627......0.0622	0.06257		21	0.0628......0.0625......0.0616	0.06230
9	0.0623......0.0626......0.0633	0.06273		22	0.0615......0.0625......0.0619	0.06197
10	0.0631......0.0631......0.0633	0.06317		23	0.0630......0.0632......0.0630	0.06307
11	0.0635......0.0630......0.0638	0.06343		24	0.0635......0.0629......0.0635	0.06330
12	0.0623......0.0630......0.0630	0.06277		25	0.0623......0.0629......0.0630	0.06273
13	0.0635......0.0631......0.0630	0.06320

Determinar:

a) Los límites de control y la línea central de la carta X. ¿Parece estar bajo control el proceso?.

b) Lo mismo con la carta R.


Apartado a)

Realizamos una recopilación de los datos ofrecidos por el enunciado del problema:

· Carta de control X, media de datos.
· Tamaño de la muestra: n = 3.
· Número de muestras: m = 25.
· Se desconoce μ y σ.

Nos piden obtener la carta de control de medias X, por lo que debemos adaptar los datos ofrecidos en la tabla (obtener el rango de dichos datos: Se resta el valor máximo con el valor mínimo dado):

Muestra	R	Media		Muestra	R	Media
1	0.0011	0.06350		14	0.0014	0.06387
2	0.0009	0.06277		15	0.0025	0.06317
3	0.0005	0.06307		16	0.0004	0.06293
4	0.0004	0.06317		17	0.0015	0.06233
5	0.0011	0.06257		18	0.0004	0.06287
6	0.0021	0.06253		19	0.0007	0.06320
7	0.0014	0.06313		20	0.0011	0.06347
8	0.0006	0.06257		21	0.0012	0.06230
9	0.001	0.06273		22	0.001	0.06197
10	0.0002	0.06317		23	0.0002	0.06307
11	0.0008	0.06343		24	0.0006	0.06330
12	0.0007	0.06277		25	0.0007	0.06273
13	0.0005	0.06320

Nos piden obtener la carta de control de medias X, cuyos límites de control son:

·

·

·

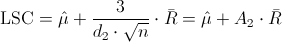
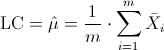
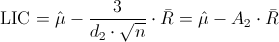
Donde A₂ y d₂, están tabulados para varios valores de n, en nuestro caso, n = 3, consultamos en la tabla:

· A₂ = 1.023
· d₂ = 1.693

Siendo:

·

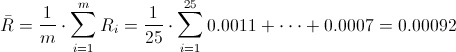
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de medias X, empezamos por la línea central:

·

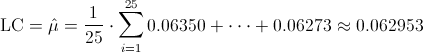
Y posteriormente, obtenemos los límites superior e inferior de control:

· LSC = μ + A₂·R = 0.062953 + 1.023·0.00092 ≈ 0.063894
· LIC = μ - A₂·R = 0.062953 - 1.023·0.00092 ≈ 0.062012

Como resumen, los límites de control para la carta X son:

· LSC = 0.063894
· LC = 0.062953
· LIC = 0.062012

Debemos representar la carta de control de medias X, pero antes, debemos obtener los límites σ y 2σ de las mismas, para su posterior análisis mediante el método: Western Electric Handbook 1956.

Para obtener los límites de advertencia σ y 2σ, existen dos formas, una es mediante una simple regla de tres, y la otra, algo más sofisticada, es obteniendo el valor de σ.

En este caso, vamos a calcular el valor de σ para obtener los límites de control de advertencia.

Sigma: σ = R/d₂ = 0.00092/1.693 ≈ 0.00054

Por lo tanto, los límites de advertencia de control 2σ son:

· X + 2·σ/√n = 0.062953 + 2·0.00054/√3 ≈ 0.063577
· X - 2·σ/√n = 0.062953 - 2·0.00054/√3 ≈ 0.062329

Para los límites de advertencia de control σ son:

· X + σ/√n = 0.062953 + 0.00054/√3 ≈ 0.063265
· X - σ/√n = 0.062953 - 0.00054/√3 ≈ 0.062641

Y en este momento, estamos en disposición de realizar la gráfica de control X:

Una vez dibujada la gráfica de control, pasamos a su análisis. Observamos que el punto 22 está fuera de los límites de control 3σ.

Por lo tanto, el proceso de la carta X, está fuera de control.


Apartado b)

En este apartado, nos piden obtener la carta de control de rangos R, cuyos límites de control son:

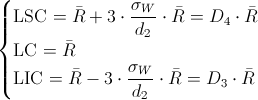
Donde D₄ y D₃, están tabulados para varios valores de n, en nuestro caso, n = 3, consultamos en la tabla:

· D₄ = 2.575
· D₃ = 0

Calculamos los límites de control de la carta R:

· LSC = D₄·R = 2.575·0.00092 = 0.002369
· LC = R = 0.00092
· LIC = D₃·R = 0·0.00092 = 0

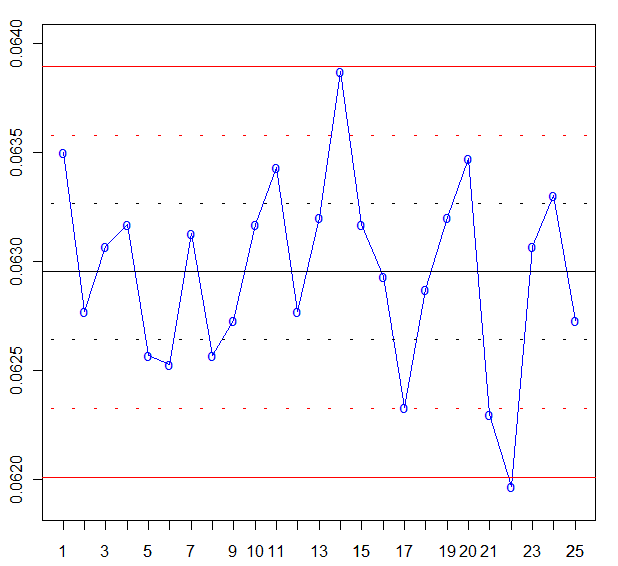
Para la representación gráfica del proceso de la carta de control R, debemos obtener los límites σ y 2·σ de las mismas para su posterior análisis mediante el método: Western Electric Handbook 1956.

Para obtener los límites de advertencia σ y 2σ, existen dos formas, una es mediante una simple regla de tres, y la otra, algo más sofisticada, es obteniendo el valor de σ.

En este caso, vamos a calcular el valor de σ para obtener los límites de control de advertencia.

Despejamos σ_w de D₄ y D₃:

·

·

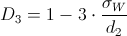
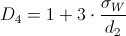
Hay que tener en cuenta, que D₄ corresponde a la parte superior de la LC y D₃ a la parte inferior de la LC.

Por lo tanto, σ_w son:

· Superior: σ_ws ≈ 0.888825
· Inferior: σ_wi ≈ 0.564333

Y el valor real de sigma está expresado:

·

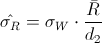
Por lo tanto:

· Superior: σ_Rs = 0.888825·0.00092/1.693 = 0.000483
· Inferior: σ_Ri = 0.564333·0.00092/1.693 ≈ 0.000307

Los límites de advertencia de control 2σ son:

· R + 2·σ_Rs = 0.00092 + 2·0.000483 = 0.001886
· R - 2·σ_Ri = 0.00092 - 2·0.000307 = 0.000306

Para los límites de advertencia de control σ son:

· R + σ_Rs = 0.00092 + 0.000483 = 0.001403
· R - σ_Ri = 0.00092 - 0.000307 = 0.000613

Y en este momento, estamos en disposición de realizar la gráfica de control R:

Una vez dibujada la gráfica de control, pasamos a su análisis. Observamos que el punto 15 está fuera de los límites de control 3σ.

Por lo tanto, el proceso de la carta R, está fuera de control.