Problema34: Probabilidad

Ej34. Una planta de producción emplea a 20 trabajadores en el turno de día, 15 en el segundo turno y 10 en el de la noche. Un consultor de control de calidad selecciona 6 de estos trabajadores para hacerles una entrevista a fondo.

Supongamos que la selección se hace de tal forma que cualquier grupo de 6 trabajadores tiene la misma probabilidad de ser seleccionado, del mismo modo que cualquier otro grupo (seleccionar 6 sin sustitución, de entre 45).

a) ¿De cuántas maneras se puede seleccionar 6 trabajadores que provengan del turno de día? ¿Cuál es la probabilidad de que los 6 trabajadores seleccionados sean del turno de día?

b) ¿Cuál es la probabilidad de que los 6 trabajadores seleccionados sean del mismo turno?

c) ¿Cuál es la probabilidad de que, al menos, dos turnos diferentes sean representados entre los trabajadores seleccionados?


Realizamos una recopilación dados por el enunciado del problema:

· Turno de día: 20 trabajadores.
· Segundo turno: 15 trabajadores.
· Turno de noche: 10 trabajadores.
· Trabajadores en total: 20 + 15 + 10 = 45 trabajadores.
· Grupos de 6 trabajadores seleccionados al azar y con la misma probabilidad de ser escogidos.

Empezamos a resolver los distintos enunciados del problema.


Apartado a)

Nos piden obtener las posibles combinaciones posibles, en grupos de 6 trabajadores, del turno de día (20 trabajadores). Para ello, empleamos la expresión combinacional:

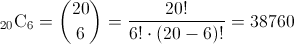
Existen, 38760 maneras posibles de seleccionar 6 trabajadores entre 20, del turno de día.

También, nos piden obtener la probabilidad de que los 6 trabajadores seleccionados al azar, sean del turno de día, esto no es más que dividir los posibles casos de seleccionar 6 trabajadores de entre 20 que corresponden al turno de día respecto a, la selección de escoger 6 trabajadores entre el total (que son 45 trabajadores repartidos entre los tres turnos).

Definimos el suceso siguiente:

· A ≡ '6 trabajadores que han sido seleccionados de entre 45, corresponda al turno de día', por lo tanto:

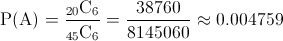
La probabilidad es bastante baja.


Apartado b)

Definimos los sucesos:

· A ≡ '6 trabajadores que han sido seleccionados de entre 45, corresponda al turno de día'.
· B ≡ '6 trabajadores que han sido seleccionados de entre 45, corresponda al segundo turno'.
· C ≡ '6 trabajadores que han sido seleccionados de entre 45, corresponda al turno de noche'.

Lo que nos piden es obtener la probabilidad de que los 6 trabajadores escogidos al azar sean del mismo turno, es decir, del turno de mañana, el segundo turno o el turno de la noche:

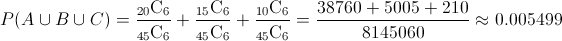
Apartado c)

En este apartado nos piden obtener la probabilidad de que los 6 trabajadores escogidos alazar no sean del mismo turno.

Esto corresponde al complemento del apartado anterior, por lo tanto:

P(6 trabajadores escogidos alazar no sean del mismo turno) = 1 - 0.005499 = 0.994501.

Observamos, que la probabilidad de seleccionar a 6 trabajadores entre 45 repartidos en tres turnos, no sean del mismo turno, es bastante alta.