Ej35. En cierta bodega, una caja contiene cuatro focos de 40W, cinco de 60W y seis 75W. Suponga que se selecciona al azar tres focos.
Determinar:
a) ¿Cuál es la probabilidad de que exactamente dos de los focos seleccionados sean de 75W?
b) ¿Cuál es la probabilidad de seleccionar un foco de cada potencia?
Realizamos una recopilación dados por el enunciado del problema:
· Focos de 40W: 4.
· Focos de 60W: 5.
· Focos de 75W: 6.
· Número de focos en total: 4 + 5 + 6 = 15 focos.
· Se seleccionan al azar, tres focos.
Empezamos a resolver los distintos apartados del problema.
Apartado a)
Nos piden obtener la probabilidad de que de los 3 focos seleccionados al azar, dos, sean de 75W.
Se puede dar la situación de obtener dos focos de 75W y uno de 40W o, dos focos de 75W y uno de 60W. Por lo tanto, la probabilidad que nos pide el enunciado obtener no es más que la suma de las dos posibilidades mencionadas anteriormente y dividirla por las posibles combinaciones de escoger tres focos entre un total de 15.
Definimos el suceso siguiente:
· A ≡ '2 de 3 focos son de 75W', por lo tanto:
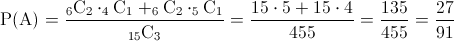
Apartado b)
Definimos los sucesos:
· B ≡ 'Seleccionar un foco de 40W, de 60W y de 75W'.
Lo que nos piden es obtener la probabilidad de escoger tres focos diferentes:
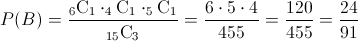





4 comentarios:
bien detallada su explicación,he salido de la duda excelente.
15C3 = 455 como se obtiene ese numero, detalladamente
Buenas:
Es la expresión de la binomial en la nomenclatura que puedes encontrar en casi todas las calculadoras científicas.
Su forma extendida es la siguiente:
(15, 3) = 15!/[3!·(15 - 3)!] = 455
Un saludo.
Y donde estan las formulas que usaron? Ni siquiera se ve que resuelven. No muestra nada del proceso.
Publicar un comentario