Ej36. En cierta gasolinera, el 40% de los clientes utilizan gasolina regular sin plomo, el 35% gasolina extra sin plomo y el 25% gasolina premium sin plomo.
De los clientes que consumen gasolina regular, sólo el 30% llenan sus tanques, de los que consumen gasolina extra, el 60% llenan sus tanques, mientras que, de los que usan premium, el 50% llenan sus tanques.
Determinar:
a) ¿Cuál es la probabilidad de que el siguiente cliente pida gasolina extra sin plomo y llene su tanque?
b) ¿Cuál es la probabilidad de llenar el tanque?
c) Si el cliente llena el tanque, ¿cuál es la probabilidad de que pida gasolina regular?, ¿extra? y ¿premium?
Realizamos una recopilación dados por el enunciado del problema:
· A1 ≡ 'Gasolina Regular sin plomo'.
· A2 ≡ 'Gasolina Extra sin plomo'.
· A3 ≡ 'Gasolina Premium sin plomo'.
· B ≡ 'Llenar el tanque'.
· P(A1) = 0.4.
· P(A2) = 0.35.
· P(A3) = 0.25.
· P(B|A1) = 0.3.
· P(B|A2) = 0.6.
· P(B|A3) = 0.5.
Ya disponemos de todos los datos necesarios para resolver los distintos apartados del problema.
Apartado a)
En este apartado nos piden obtener la probabilidad de la intersección entre los sucesos de repostar con gasolina extra sin plomo y llenar el tanque de combustible.
Por definición:
Apartado b)
Nos piden hallar la probabilidad del suceso B, llenar el tanque, para tal fin, empleamos la expresión de la probabilidad total:
Apartado c)
Una vez obtenida la probabilidad total en el apartado anterior, empleamos la expresión del Teorema de Bayes para resolver los distintos subapartados expuestos:
· Para la gasolina Regular sin plomo:

· Para la gasolina Extra sin plomo:
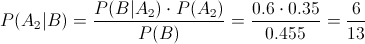
· Para la gasolina Premium sin plomo:
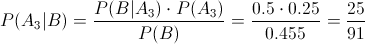





3 comentarios:
hola, de que libro es este problema??, Gracias por el desglose, muy útil.
Excelente explicación, gracias
Devore (2008)
Publicar un comentario