Problema6: Cartas de Control

Ej6. El fabricante de ordenadores personales, quiere diseñar una carta de control de defectos por máquina al final del montaje.

Para ello, toma unidades de inspección constituidas, cada una, por una muestra aleatoria de cinco ordenadores. Los resultados de tal muestreo están reseñados en la tabla que sigue:

Unidad	Número de Defectos		Unidad	Número de Defectos
1	10		11	9
2	12		12	5
3	8		13	7
4	14		14	11
5	10		15	12
6	16		16	6
7	11		17	8
8	7		18	10
9	10		19	7
10	15		20	5

Determinar:

a) Los límites de control y la línea central de la carta U.

b) Traza la gráfica de control de la citada carta, ¿está el proceso bajo control?.


Apartado a)

Realizamos una recopilación de los datos ofrecidos por el enunciado del problema:

· Carta de control U, número de defectos por unidad.
· Tamaño de la muestra: n = 5.
· Número de muestras: m = 20.

Nos piden obtener la carta de control de defectos por unidad U, por lo que debemos adaptar los datos ofrecidos en la tabla en defectos por unidad (dividir el número de defectos entre el tamaño de la muestra, en este caso, por 5):

Unidad	Nº de Defectos por Unidad		Unidad	Nº de Defectos por Unidad
1	2.0		11	1.8
2	2.4		12	1.0
3	1.6		13	1.4
4	2.8		14	2.2
5	2.0		15	2.4
6	3.2		16	1.2
7	2.2		17	1.6
8	1.4		18	2.0
9	2.0		19	1.4
10	3.0		20	1.0

Y en estos momentos, estamos en disposición de obtener los límites de control:

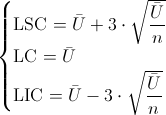
Siendo:

·

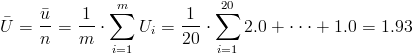
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de defectos por unidad, U:

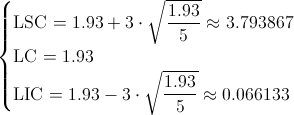
Apartado b)

Debemos representar la carta de control U, del número de defectos por unidad, pero antes, debemos obtener los límites σ y 2σ de la misma, para su posterior análisis mediante el método: Western Electric Handbook 1956.

Para obtener los límites de advertencia σ y 2σ, existen dos formas, una es mediante una simple regla de tres, y la otra, algo más sofisticada, es obteniendo el valor de σ.

En este caso, usaremos la regla de tres para obtener los límites de control de advertencia.

- Para el límite superior:

(LSC - LC)/3 = (3.793867 - 1.93)/3 = 0.621289

Por lo tanto, los límites de advertencia de control 2σ son:

· u + 2·σ = 1.93 + 2·0.621289 = 3.172578

Para los límites de advertencia de control σ son:

· u + σ = 1.93 + 0.621289 = 2.551289

- Para el límite inferior:

(LC - LIC)/3 = (1.93 - 0.066133)/3 = 0.621289

Por lo tanto, los límites de advertencia de control 2σ son:

· u - 2·σ = 1.93 - 2·0.621289 = 0.687422

Para los límites de advertencia de control σ son:

· u - σ = 1.93 - 0.621289 = 1.308711

Podemos comprobar, que tanto para el límite superior como para el inferior, el valor es el mismo, esto es así ya que existe la misma distancia entre la línea central, LC, con el límite superior, LSC, y el límite inferior, LIC.

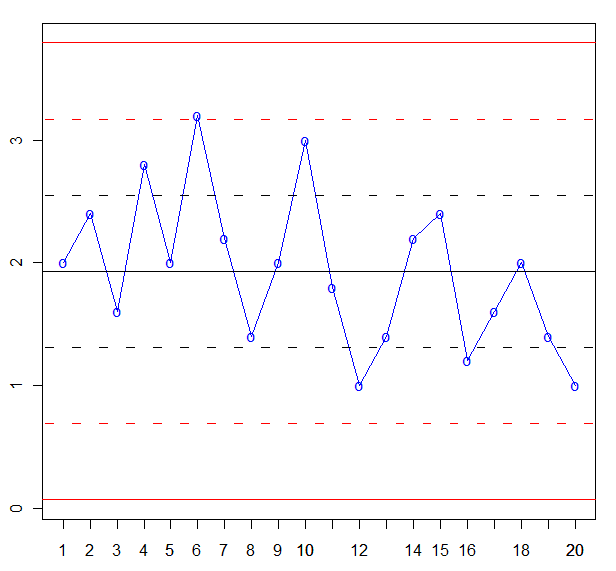
Y en este momento, estamos en disposición de realizar la gráfica de control U:

Una vez dibujada la gráfica de control, pasamos a su análisis. En un primer vistazo observamos que todos los puntos están dentro de los límites de control 3σ. Aparte, la gráfica de control cumple con todas las premisas de la regla, por lo tanto, el proceso está bajo control.