Ej33. Estudiamos la resistencia de piezas de cemento a medida que va aumentando el tiempo de fraguado y aceptamos como modelo de dicha resistencia para una pieza escogida al azar, una distribución Normal con media 25 y desviación típica 3.
a) ¿Qué proporción p de piezas tienen una resistencia superior a 28?.
b) Hallar el valor de la resistencia por debajo del cual se encuentra el 97.5% de las piezas.
Sea la variable aleatoria X, resistencia de piezas de cemento. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para hallar los apartados requeridos.
Cuya media es: 25 y la desviación estándar: 3.
Por lo tanto, la variable continua aleatoria, sigue una distribución Normal: X ~ N(25, 3)
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.
Apartado a)
Tenemos que resolver:
Tipificamos a la Normal:
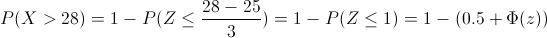
Simplificamos:
Buscamos en la tabla de la Normal dicho valor y resolvemos este apartado:
Por lo tanto, la proporción de piezas, p, que tienen una resistencia superior a 28 es de 0.1587, una probabilidad baja.
Apartado b)
En este problema, nos dan los datos de la probabilidad y debemos hallar el valor de la variable aleatoria X que lo satisfaga.
Tenemos: P(X < x) = 0.975
Tipificamos:
Despejamos:
Buscamos en la tabla, que dispone este blog para los valores Normales tipificados, el valor 0.475 que de un z válido.
Es este caso, z = 1.96
Por lo tanto, el valor de la resistencia será:
Despejamos x y obtenemos la solución a este problema: x ≥ 30.88.

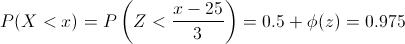
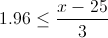




2 comentarios:
en b el resultado es 30,88
Buenas:
Efectivamente, el resultado en el Apartado b) es de 30.88 ya que confundí, al realizar el ejercicio, la media de la variable aleatoria, no era 28 sino 25.
Ya está corregido.
Muchas gracias por tu corrección y por tu comentario.
Publicar un comentario