Problema41: Probabilidad

Ej41. Una depuradora de aguas residuales utiliza dos test de diagnóstico de contaminación accidental: el primero está basado en el control de la flora de bacterias, mientras que el segundo en la medición del nivel de oxígeno en el agua.

En el caso de estar presente la contaminación, el test bacteriano lo detecta en el 90% de los casos, mientras que el test de oxígeno lo detecta en el 80% de los casos. Además como es habitual, el test diagnostica contaminación accidental cuando no es cierto.

Eso ocurre con una probabilidad de 0.05 para el test bacteriano y una probabilidad de 0.02 para el test de oxígeno.

Conociendo que la probabilidad de un episodio de contaminación accidental es 0.08, y suponemos que los tests son independientes, determinar:

a) Calcular la probabilidad de que el test bacteriano indique (erróneamente o no) que hay un episodio de contaminación accidental.

b) Calcular la probabilidad de que el test de oxígeno indique (erróneamente o no) que hay un episodio de contaminación accidental.

c) Calcular la probabilidad de que los dos test indiquen simultáneamente contaminación accidental.

d) Probabilidad de que, sabiendo que el test de oxígeno ha detectado contaminación, haya ocurrido realmente un episodio de contaminación.


Realizamos una recopilación de datos dados por el enunciado del problema:

· X₁ ≡ 'Control de la flora de bacterias'.
· X₂ ≡ 'Medición del nivel de oxígeno en el agua'.
· E ≡ 'Contaminación accidental'.

· P(X₁|E) = 0.9.
· P(X₂|E) = 0.8.
· P(X₁|Ē) = 0.05.
· P(X₂|Ē) = 0.02.
· P(E) = 0.08.

· Ambos test, X₁ y X₂, son independientes.

Pasamos a resolver los distintos apartados del problema.


Apartado a)

En este apartado debemos obtener la probabilidad del test bacteriano, lo hacemos por la Ley de la Probabilidad Total:

P(X₁) = P(X₁|E)·P(E) + P(X₁|Ē)·P(Ē) = 0.9·0.08 + 0.05·(1-0.08) = 0.118

La probabilidad de que el test bacteriano indique contaminación accidental, es de 0.118.

Apartado b)

Este apartado se procede igual que en el anterior pero esta vez, con el test de medición del nivel de oxígeno en el agua:

P(X₂) = P(X₂|E)·P(E) + P(X₂|Ē)·P(Ē) = 0.8·0.08 + 0.02·(1-0.08) = 0.0824

La probabilidad de que el test de medición del nivel de oxígeno en agua indique contaminación accidental, es de 0.0824.


Apartado c)

Debemos obtener la probabilidad de que los dos test indiquen contaminación accidental:

P(X₁ ∩ X₂)

Al ser test independientes:

P(X₁ ∩ X₂) = P(X₁)·P(X₂) = 0.118·0.0824 ≈ 0.009723

Podemos observar, que la probabilidad de que ambos test, indiquen contaminación accidental, es muy baja.


Apartado d)

En este problema, nos piden obtener la siguiente probabilidad (Ley de Bayes):

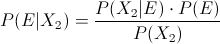
En estos momentos, disponemos de todos los datos necesarios para resolver este problema:

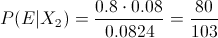
Por lo tanto, la probabilidad de que sabiendo que el test de oxígeno ha detectado contaminación, haya ocurrido realmente un episodio de contaminación, es de, aproximadamente, 0.776699.