Problema34: VAD

Ej34. La variable aleatoria X que representa la duración (en horas) de las conexiones desde un puesto a dominios de la red “no relacionados directamente con el trabajo” viene dada por la siguiente función de densidad:

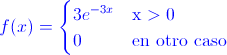
Hallar:

a) Si un empleado es pillado, la empresa le sanciona con una cantidad Z = X² euros, ¿cuál es la probabilidad de que un sancionado tenga que pagar más de 5 euros?.

b) ¿Cuál es la probabilidad de que un empleado esté entre media hora y tres cuartos de hora conectado a la red “sin trabajar”?.

c) El coste (en euros) para la empresa viene dado por la variable aleatoria: Y = 2 + bX. Calcula el valor de b para que el 95% de las conexiones tengan un coste que no supere los 6 euros.


Vamos a obtener la función de distribución acumulada.

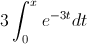
Hacemos un cambio de variable:

· m = -3t
· dm = -3dt

Aplicamos el cambio de variable:

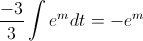
Deshacemos el cambio de variable y resolvemos:

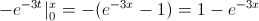
Por lo tanto, la función acumulada quedará:

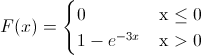
Pasamos a resolver los distintos apartados del problema.


Apartado a)

Necesitamos resolver la siguiente probabilidad:

P(Z > 5)

En enunciado nos indica que Z = X², despejamos:

P(Z > 5) = P(X² > 5) = P(X > ±√5)

Teniendo en cuenta que para valores negativos, el valor de la variable aleatoria es cero, debemos resolver, empleando la función de distribución acumulada:

P(Z > 5) = P(X > √5) = 1 - P(X ≤ √5) = 1 - (1 - e^-3√5) = e^-3√5 ≈ 0.001221

Por lo tanto, que un empleado sea sancionado tenga que pagar más de 5€ es de, aproximadamente, 0.001221, una probabilidad baja.


Apartado b)

La variable aleatoria está determinada en horas, por lo que pasamos los datos a dicha magnitud:

30 minutos = 0.5 horas.
45 minutos = 0.75 horas.

Y la probabilidad que debemos obtener, es la siguiente:

P(0.5 < .X < .0.75) = F(0.75) - F(0.5) = (1 - e^-3·0.75) - (1 - e^-3·0.5) = -e^-2.25 + e^-1.5 ≈ 0.117731

Por lo tanto, la probabilidad de que un trabajador esté entre media hora y tres cuartos de hora conectado a la red sin trabajar es de, aproximadamente, 0.117731.

Apartado c)

En este apartado no dan una función que contiene nuestra variable aleatoria continua X, ésta es:

Y = 2 + b·X

Y la probabilidad que debemos obtener es:

P(Y ≤ 6)

Sustituimos:

P(Y ≤ 6) = P(2 + b·X ≤ 6)

Despejamos la variable aleatoria X, en función del parámetro que debemos obtener, b:

X ≤ 4/b

Una vez obtenido el valor de X en función de b y sabiendo la probabilidad, 0.95, obtenemos el parámetro b:

P(X ≤ 4/b) = F(4/b) = 1 - e^-3·4/b = 1 - e^-12/b = 0.95

Despejamos:

e^-12/b = 0.05

Aplicamos logaritmo neperiano:

-12/b = Ln(0.05)

Despejamos el parámetro b para obtener su valor y resolver este apartado:

b = -12/Ln(0.05) ≈ 4.005698

Por lo tanto, el valor del parámetro b para que el 95% de las conexiones tengan un coste que no supere los 6€ es de, aproximadamente, 4.005698.