Ej42. Una empresa compra determinada pieza a dos fábricas Q y R, comprando a Q, 5 veces lo que compra a R. Además, el 10% de las piezas de la fábrica Q y el 16% de las piezas de la fábrica R llegan a la empresa en mal estado. Se pide:
a) Hallar el porcentaje de piezas que llegan en mal estado a la empresa.
b) Si una pieza está en mal estado, hallar la probabilidad de que sea de la fábrica Q.
Realizamos una recopilación de datos dados por el enunciado del problema:
· Q ≡ 'Pieza de la fábrica Q'.
· R ≡ 'Pieza de la fábrica R'.
· M ≡ 'Piezas que llegan a la empresa en mal estado'.
· P(M|Q) = 0.10.
· P(M|R) = 0.16.
· P(Q) = 5/6.
· P(R) = 1/6.
Pasamos a resolver los distintos apartados del problema.
Apartado a)
En este apartado debemos obtener la probabilidad de que lleguen a la empresa piezas en mal estado, para ello, empleamos la Ley de Probabilidad Total:
El porcentaje de piezas que llegan en mal estado a la empresa, es de 0.11·100 = 11%.
Apartado b)
En este problema, nos piden obtener la siguiente probabilidad (Ley de Bayes):
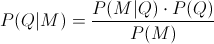
En estos momentos, disponemos de todos los datos necesarios para resolver este problema:
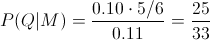
Por lo tanto, la probabilidad de que dado que una pieza está en mal estado sea de la fábrica Q, es de, aproximadamente, 0.757576.





0 comentarios:
Publicar un comentario