Problema35: VAC

Ej35. Una empresa compra determinada pieza a dos fábricas Q y R, el porcentaje de piezas que llegan en mal estado a la empresa es del 11%.

Si se toman al azar 500 piezas de un pedido, hallar la probabilidad de que al menos 440 estén en buen estado.


Sea la variable aleatoria discreta X, piezas que llegan a la empresa en buen estado. Realizamos en resumen de los datos que nos ofrece el enunciado del problema:

La variable aleatoria discreta X, sigue una distribución binomial: X ~ B(500, 1-0.11) = B(550, 0.89).

Comprobaremos, si se puede aproximar a la normal, para ello, se deben cumplir las siguientes condiciones:

1. n·p ≥ 5: 500·0.89 = 445 ≥ 5 OK.

2. n·q ≥ 5: 500·0.11 = 55 ≥ 5 OK.

Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:

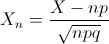
Por lo tanto: X ~ N(n·p, √(n·p·q)) ≈ N(445, 6.996428).

Debemos calcular: P(X ≥ 440) = 1 - P(X < .440), pero antes, debemos aplicar la corrección por continuidad, por lo tanto, tenemos: 1 - P(X < .440.5 ).

Tipificamos:

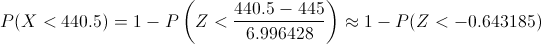
Operamos:

P(X < .440.5) = 1 - P(Z < .-0.643185) = 1 - [1 - (0.5 + Φ(0.643185))] = 0.5 + Φ(0.643185)

En este caso, no se dispone del valor exacto en las tablas que están en Aqueronte para su consulta, por lo tanto, interpolamos linealmente:

..0.64........0.643185.......0.65
0.2389............P............0.2422

De donde:

0.64 - 0.65.-> 0.2389 - 0.2422
0.64 - 0.643185.-> 0.2389 - P

Calculamos:

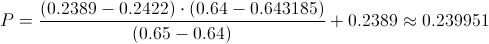
Sustituyendo valores, obtenemos la solución a este problema:

P(X < .440.5) = 0.5 + Φ(0.643185) = 0.5 + 0.239951 = 0.739951

Por lo tanto, la probabilidad de que al menos 440 de entre 500 piezas que llegan a la empresa, estén en buen estado, es de 0.739951.