Problema36: VAC

Ej36. El peso de las ciruelas es una variable aleatoria con función de densidad f(x) = k para 6 < .x < .10 en gramos. Se pide:

a) Encontrar el valor de k para que f(x) sea una función de densidad.

b) El peso medio de las ciruelas y su desviación típica.

c) Las ciruelas se separan en dos grupos, las de peso menor que a y las de peso mayor que a. Encontrar el valor de a que maximiza el beneficio si cada ciruela chica se vende a 0.2 euros cada unidad y las grandes a 0.025·a euros cada unidad.


Apartado a)

Empleamos la expresión de función de densidad de probabilidad:

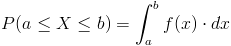
Para los intervalos expuestos en el enunciado del problema, en este caso:

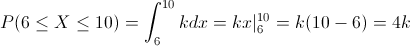
Para que una variable aleatoria continua posea una función de densidad de probabilidad, tienen que cumplirse las siguientes condiciones:

1. f(x) > 0,...para todo x.

2.

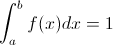
La función f(x) es mayor que cero, por lo que nos queda, satisfacer la primera condición:

4·k = 1

Y así, obtenemos el valor de k y la solución del problema, para que f(x) sea una función de densidad de probabilidad, el valor de k es de 1/4.

Por lo tanto, la función de densidad de la variable aleatoria continua X queda:

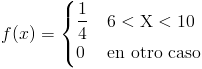
Obtendremos también, la función de distribución acumulada:

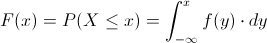
En nuestro caso, el intervalo que tenemos que realizar cálculos es: 6 ≤ X ≤ 10:

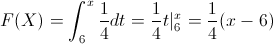
La función de distribución acumulada queda tal y como se muestra a continuación:

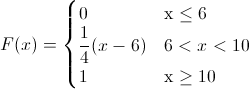
Apartado b)

En este apartado, debemos calcular la esperanza y la varianza de la variable aleatoria continua, X.

Para el cálculo de la esperanza, empleamos la siguiente expresión:

Por lo tanto, la esperanza de X, será:

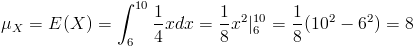
Y para la varianza, se empleará la siguiente expresión:

· Var(X) = E(X²) - [E(X)]²

Por lo tanto:

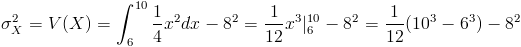
Simplifico:

Por lo tanto, la varianza es:

σ = √(4/3) ≈ 1.154701

Apartado c)

Recopilo información de este apartado:

· Peso menor que a: Se vende a 0.2.
· Peso mayor que a: Se vende a 0.025·a.

Suponemos que el parámetro a se encuentra en el intervalo: 6 < .a < .10. Esta suposición se comprobará al final del problema.

Por lo tanto, las probabilidades, empleando la función de distribución acumulada:

· P(X < .a) = 1/4 · (a - 6)
· P(X >.a) = 1 - P(X ≤.a) = 1 - 1/4 · (a - 6) = 2.5 - a/4

Y lo que nos piden obtener es la siguiente probabilidad:

P(X) = 0.2·P(X < .a) + 0.025·a·P(X > a) = 0.2·(1/4)·(a-6) + 0.025a·(2.5-a/4)

Opero y simplifico:

P(X) = 0.05a - 0.3 + 0.0625a - 0.00625a² = -0.00625a² + 0.1125a -0.3

Para obtener el valor del parámetro a, obtenemos la primera derivada de la función e igualamos a cero:

P'(X) = -0.0125·a + 0.1125 = 0

Por lo tanto el parámetro a tiene el valor de: a = 9.

Obtengo la segunda derivada para cerciorarnos que es un máximo (máximo beneficio) de la función:

P''(X) = -0.0125 < .0

Es negativo, por lo que el beneficio es máximo para un valor de a de 9.

Podemos comprobar, que la suposición que hicimos al inicio del problema de que el parámetro a debe estar entre el intervalo: 6 < .a < .10, es correcta.