Problema33: Estimación y Pruebas de Hipótesis

Ej33. Dos algoritmos A y B permiten simular cierto proceso. En 10 simulaciones, realizadas con cada uno de ellos, se obtuvieron los siguientes tiempos de ejecución por cada simulación:

A:	7..	10..	8..	9..	6.5..	8..	7..	7.5..	9..	8
B:	7	7	6	5.5	7	8	6.5	7	7	9

Determinar:

a) ¿Proporcionan los datos la evidencia su ficiente, al nivel de signi cación α = 0.05, para concluir que hay diferencias entre los tiempos medios de ejecución de ambos algoritmos?

NOTA: Supóngase normalidad e igualdad de varianzas en los tiempos de ejecución.

b) ¿Cuál es el valor P de esta prueba?.


En este problema, nos dan los datos de dos muestras aleatorias, por lo que tenemos que obtener la media de cada algoritmo.

Para obtener la media:

Por lo tanto:

· A:

· B:

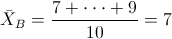
Para obtener la cuasi varianza:

Por lo tanto, la cuasi desviación típica:

· A: S_cA ≈ 1.080123
· B: S_cB ≈ 0.971825

Pasamos a resolver los distintos apartados del problema.


Apartado a)

La prueba de hipótesis que plantea el enunciado del problema es:

Es un contraste de diferencia de medias con desviación estándar desconocidas e iguales, el estadístico es:

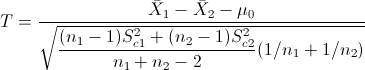
Obtenemos el valor del estadístico:

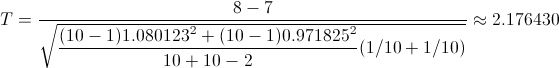
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

T ≤ - t_α/2,n1+n2-2, T ≥ t_α/2,n1+n2-2

Para un nivel de significación de: α = 0.05, tenemos, en la tabla t-Student:

· t_α/2,n1+n2-2 = t_{0.05/2,10+10-2}=t_0.025,18

Buscamos el valor en la tabla t-Student, y obtenemos: 2.1009.

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 2.176430 está fuera del intervalo que compone la región crítica, (-2.1009, 2.1009), por lo tanto, rechazamos la hipótesis nula.

Esto quiere decir que, existen evidencias significativas de que la diferencia de medias son distintas, ya que se acepta la hipótesis alternativa.


Apartado b)

En este apartado, nos piden obtener el p-valor de la prueba del apartado anterior, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen dos regiones críticas, por lo tanto, tenemos dos colas de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = 2 · P(T > |t|) = 2 · P(T > 2.176430)

Buscamos en las tablas de la t-Student, pero no encontramos el valor exacto para 2.176430 con 18 grados de libertad, por lo que podemos dar un intervalo donde se encuentre el p-valor:

En nuestro caso, el valor 2.176430 se encuentra comprendido entre los niveles de significancia:

0.0125 < .T < .0.025

Como son áreas de cola, el p-valor estará comprendido entre los valores:

0.025 < .p-valor< .0.05

También, podemos dar un valor aproximado del p-valor mediante interpolación lineal:

..0.025...........T...........0.0125
2.1009....2.176430....2.4450

De donde:

0.025 - 0.0125.-> 2.1009 - 2.4450
0.025 - T.-> 2.1009 - 2.176430

Calculamos:

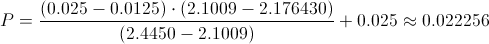
Sustituimos y obtenemos el p-valor:

p-valor = 2 · P(T > 2.176430) = 2·0.022256 = 0.044512

Como el p-valor es menor que el nivel de significación, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa.