Ej39. Sea X una variable aleatoria continua que mide la longitud de una determinada pieza, cuya función es:
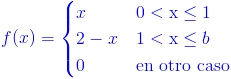
Hallar:
a) Obtener el valor de b para que sea una función de densidad.
b) Obtener la función de distribución acumulada.
Apartado a)
Empleamos la expresión de función de densidad de probabilidad:
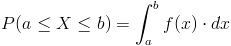
En nuestro caso, debemos realizar el estudio en dos intervalos.
· Primer intervalo: 0 < .x ≤ 1:
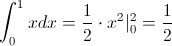
· Segundo intervalo: 1 < .x ≤ b:
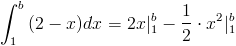
Despejamos y obtenemos:
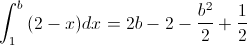
Para que una variable aleatoria continua posea una función de densidad de probabilidad, tienen que cumplirse las siguientes condiciones:
1. f(x) > 0,...para todo x.
2.
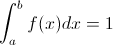
La función f(x) es mayor que cero, por lo que nos queda, satisfacer la primera condición:
-(1/2)·b + 2·b - 1 = 1
Despejamos:
b2 - 4b + 2 = 0
Obtenemos una ecuación cuadrática, en este caso, es fácil factorizarla:
(b-2)2 = 0
Por lo tanto, el valor del parámetro b para que la función dada sea una función de probabilidad, es de 2.
La función de densidad de la variable aleatoria continua X queda:
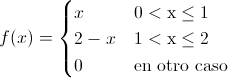
Apartado b)
Empleamos la expresión de función de distribución acumulada:
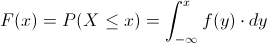
En nuestro caso, debemos realizar el estudio en dos intervalos.
· Primer intervalo: 0 < .x ≤ 1:
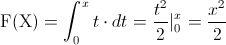
· Segundo intervalo: 1 < .x ≤ 2:
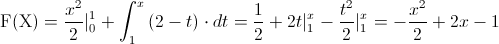
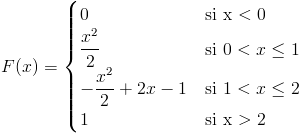





2 comentarios:
buenas tardes
muchas gracias por este aporte tan grande al aprendizaje de la estadistica.
}
tengo una pregunta: como se puede graficar la funcion de densidad de esta función, como hallar el valor esperado en funciones como esta donde f(x) toma mas de 2 valores, es decir x y 2-x dependiendo de los intervalos
quedo atenta
muchas gracias
Buenas:
Para empezar, deberás decir en que intervalos está definida la función de densidad de probabilidad para poder dibujarla.
De todas formas, si te miras la teoría en este capítulo: Variables Aleatorias Continuas y Distribuciones de Probabilidad, encontrarás cómo obtener la esperanza, varianza, etc.
Y además, los primeros 10 ejercicios (más o menos), encontrarás ejercicios de cómo se representan este tipo de funciones mediante un lenguaje estadístico llamado: R.
Un saludo y gracias por tu comentario.
Publicar un comentario