Problema54: Probabilidad

Ej54. El 25% de los aparatos que llegan a cierto servicio técnico tienen garantía. Entre los
que no tienen garantía, un 20% ya fueron reparados en otra ocasión. Finalmente, el 5% de los aparatos tienen garantía y además ya fueron reparados en otra ocasión.

Determinar:

a) ¿Qué porcentaje de los aparatos que llegan a este servicio ya fueron reparados en otra ocasión?

b) ¿Qué porcentaje no fueron reparados en otra ocasión y además no tienen garantía?

c) Un aparato que acaba de llegar ya fue reparado en otra ocasión. ¿Qué probabilidad hay de que
tenga garantía?


Realizamos una recopilación de datos dados por el enunciado del problema:

· E ≡ 'Tienen garantía'.
· R ≡ 'Ya han sidos reparados anteriormente'.

· P(E) = 0.25.
· P(R|Ē) = 0.20.
· P(E∩R) = 0.05.

Pasamos a resolver los apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de ser reparados:

P(R) = P(R|Ē)·P(Ē)+P(R|E)·P(E)

Obtenemos la probabilidad condicional que nos falta:

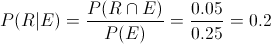
Ya disponemos de todos los datos necesarios para resolver este apartado:

P(R) = P(R|Ē)·P(Ē)+P(R|E)·P(E) = 0.2(1-0.25)+0.2·0.25 = 0.2

Por lo tanto, el porcentaje de aparatos que llegan a este servicio técnico no fueron reparados anteriormente es del 20%.


Apartado b)

Debemos obtener la siguiente probabilidad:

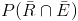
Al ser sucesos independientes:

Sustituimos valores:

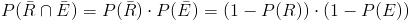
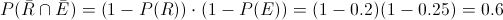
Por lo tanto, el porcentaje de aparatos que llegan a este servicio técnico no fueron reparados anteriormente y no tienen garantía es del 60%.


Apartado c)

Para resolver este apartado, debemos emplear la Ley de Bayes:

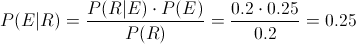
Por lo tanto, el porcentaje de aparatos que tengan garantía dados que ya fueron reparados anteriormente es del 25%.