Problema36: VAD

Ej36. Una empresa electrónica observa que el número de componentes que fallan antes de cumplir 100 horas de funcionamiento es una variable aleatoria de Poisson.

Si el número promedio de estos fallos es ocho, obtener:

a) ¿Cuál es la probabilidad de que falle un componente en 25 horas?

b) ¿Y de que fallen no más de dos componentes en 50 horas?

c) ¿Cuál es la probabilidad de que fallen por lo menos diez en 125 horas?.


Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Número de componentes que fallan antes de cumplir 100 horas de funcionamiento'.
· Tamaño de la muestra: n = 100.
· La variable aleatoria X sigue una distribución Poisson: X ~ P(8).

Pasamos a resolver los apartados ofrecidos por el enunciado del problema.


Apartado a)

En este apartado, el tamaño de la muestra cambia para pasar a ser 25 horas. Hay que tener en cuenta que nuestro parámetro λ (λ = 8) es para 100 horas de funcionamiento, por lo que interpretamos que dicho parámetro es lineal y obtenemos el valor medio para las horas de funcionamiento de este apartado:

100 --- 8
.25..--- λ

Por lo tanto, el número promedio de fallos para 25 horas es de:

· λ = (25·8)/100 = 2

Y la probabilidad que debemos hallar es la siguiente:

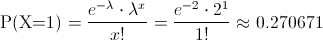
La probabilidad de que falle un componente en 25 horas es de, aproximadamente, 0.270671.


Apartado b)

Al igual que ne el apartado anterior, debemos adaptar el parámetro promedio de fallos:

100 --- 8
.50..--- λ

Por lo tanto, el número promedio de fallos para 50 horas es de:

· λ = (50·8)/100 = 4

Y la probabilidad que debemos hallar es la siguiente:

P(X ≤ 2) = P(X=0) + P(X=1) + P(X=2)

Por lo tanto:

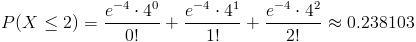
La probabilidad de que fallen al menos dos componentes en 50 horas es de, aproximadamente, 0.238103.


Apartado c)

Al igual que ne el apartado anterior, debemos adaptar el parámetro promedio de fallos:

100 --- 8
125..--- λ

Por lo tanto, el número promedio de fallos para 125 horas es de:

· λ = (125·8)/100 = 10

Y la probabilidad que debemos hallar es la siguiente:

P(X ≥ 10) = 1 - P(X < .10) = 1 - [P(X=0) + P(X=1) +···+ P(X=7) + P(X=8) + P(X=9)]

Por lo tanto:

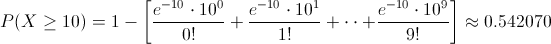
La probabilidad de que fallen al menos diez componentes en 125 horas es de, aproximadamente, 0.542070.