Problema38: VAD

Ej38. Un lote contiene 100 piezas de un proveedor de tubería local y 200 unidades de un proveedor de tubería del estado vecino.

Si se seleccionan cuatro piezas al azar y sin reemplazo, determinar:

a) ¿Cuál es la probabilidad de que todas sean del proveedor local?

b) ¿Cuál es la probabilidad de que dos o más piezas de la muestra sean del proveedor local?

c) ¿Cuál es la probabilidad de que al menos una pieza de la muestra sea del proveedor local?

Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Nº de tuberías procedentes del proveedor local'.
· La variable aleatoria X sigue una distribución Hipergeométrica: X ~ HG de parámetros:
· Número total de tuberías: N = 100+200 = 300.
· Tamaño de la muestra: n = 100. (Número total de tuberías del proveedor local)
· Número total de seleccionados aleatoriamente: r = 4 (sin reemplazamiento).

Pasamos a resolver los distintos apartados que nos ofrece el problema.


Apartado a)

Debemos hallar la siguiente probabilidad:

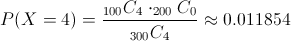
Por lo tanto, la probabilidad de que todas las tuberías provengan del proveedor local es de, aproximadamente, 0.011854.


Apartado b)

Para este apartado, debemos obtener la siguiente probabilidad:

P(X ≥ 2) = 1 - P(X < .2) = 1 - [P(X=0) + P(X=1)]

Sustituimos valores y obtenemos la solución a este apartado:

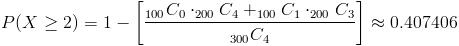
Por lo tanto, la probabilidad de escoger más o igual a dos tuberías del proveedor local es de, aproximadamente, 0.407406.


Apartado c)

Para este apartado, debemos obtener la siguiente probabilidad:

P(X ≥ 1) = 1 - P(X < .1) = 1 - P(X=0)

Sustituimos valores y obtenemos la solución a este apartado:

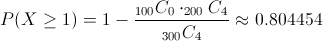
Por lo tanto, la probabilidad de escoger más o igual a una tubería del proveedor local es de, aproximadamente, 0.804454.