Ej39. Supongamos que el número de imperfecciones en un alambre delgado de cobre sigue una distribución Poisson con una media de 2.3 imperfecciones por milímetro.
a) Determine la probabilidad de 2 imperfecciones en un milímetro de alambre.
b) Determine la probabilidad de 10 imperfecciones en 5 milímetros de alambre.
c) Determine la probabilidad de al menos una imperfección en 2mm de alambre.
Realizamos una recopilación de datos del enunciado del problema:
· X ≡ 'Número de imperfecciones en un alambre delgado de cobre'.
· Tamaño de la muestra: n = 1mm.
· La variable aleatoria X sigue una distribución Poisson: X ~ P(2.3).
Pasamos a resolver los apartados ofrecidos por el enunciado del problema.
Apartado a)
La probabilidad que debemos obtener es la siguiente:
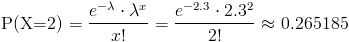
La probabilidad de que existan dos imperfecciones en un alambre delgado de cobre es de, aproximadamente, 0.265185.
Apartado b)
Debemos adaptar el parámetro promedio de imperfecciones ya que para este apartado no exponen un tamaño de 5mm:
1 --- 2.3
5..--- λ
Por lo tanto, el número medio de imperfecciones para 5mm de cable es de:
· λ = (5·2.3)/1 = 11.5
Y la probabilidad que debemos hallar es la siguiente:
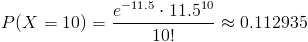
La probabilidad de que existan diez imperfecciones en un alambre de cobre por 5mm es de, aproximadamente, 0.112935.
Apartado c)
Al igual que ne el apartado anterior, debemos adaptar el parámetro promedio de imperfecciones:
1 --- 2.3
2..--- λ
Por lo tanto, el número medio de imperfecciones para 2mm de cable es de:
· λ = (2·2.3)/1 = 4.6
Y la probabilidad que debemos hallar es la siguiente:
Por lo tanto:
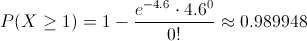
La probabilidad de que existan al menos una imperfección por 2mm de alambre de cobre es de, aproximadamente, 0.989948, una probabilidad bastante alta.





0 comentarios:
Publicar un comentario