Ej40. La contaminación constituye un problema en la fabricación de discos de almacenamiento óptico. El número de partículas de contaminación que ocurre en un disco óptico tiene una distribución de Poisson y el número promedio de partículas por centímetro cuadrado de superficie del disco es 0.1.
El área de un disco bajo estudio es 100 centímetros cuadrados. Determinar:
a) Encuentre la probabilidad de que ocurran 12 partículas en el área del disco bajo estudio.
b) La probabilidad de que ocurran cero partículas en el área del disco bajo estudio.
c) Determine la probabilidad de que 12 o menos partículas ocurran en el área del disco bajo estudio.
Realizamos una recopilación de datos del enunciado del problema:
· X ≡ 'Número de partículas de contaminación en un disco óptico'.
· Tamaño de la muestra: n = 1cm2.
· Área de estudio: 100cm2.
· La variable aleatoria X sigue una distribución Poisson: X ~ P(0.1).
Los apartados que debemos resolver están basados en el área de estudio especificada, por lo que debemos adaptar nuestro parámetro promedio:
...1....--- 0.1
100..--- λ
Por lo tanto, el número medio de contaminación de partículas para 100cm2 es de:
· λ = (100·0.1)/1 = 10
Pasamos a resolver los apartados ofrecidos por el enunciado del problema.
Apartado a)
La probabilidad que debemos obtener es la siguiente:
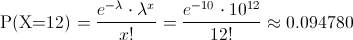
La probabilidad de que existan doce partículas de contaminación en los discos ópticos es de, aproximadamente, 0.094780.
Apartado b)
La probabilidad que debemos hallar es la siguiente:
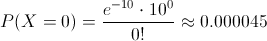
La probabilidad de que no existan partículas de contaminación en los discos ópticos es de, aproximadamente, 0.000045, es decir, es muy poco probable que no hayan partículas de este tipo en el área de los discos ópticos.
Apartado c)
La probabilidad que debemos hallar es la siguiente:
Para resolver este apartado, al ser muy tedioso, emplearemos el software R:
> ppois(c(12),10)
[1] 0.7915565
La probabilidad de que existan menos o igual de doce partículas de contaminación en los discos ópticos es de, aproximadamente, 0.791556.





2 comentarios:
hola, esta bien tu resultado., pero como lo planteaste esta mal:
X= 12
λ = 10
P(x ocurrencias; λ) = e^(-λ) λ^x=
X!
P(0;10) = (〖2.7182〗^(-10)) X (〖10〗^0 )= (0.00004539) X (1) = 0.00004539= 00004539
0! 1 1
muchas gracias por ayudarme con el primero
saludos!!!!
Buenas:
Es cierto, me equivoqué en el parámetro promedio, en vez de poner 10 puse 12 aunque las operaciones consideré el 10 es por ello que el resultado estaba bien.
Un fallo al escribir las ecuaciones en LaTeX.
Gracias por el apunte y me alegro que te sirvan estos ejemplos, un saludo.
Publicar un comentario