Ej41. Una prueba consta de 200 preguntas de verdadero o falso, para un sujeto que respondiese al azar, determinar cuál sería la probabilidad de que acertase:
a) 50 preguntas o menos.
b) Más de 50 y menos de 100.
c) Más de 120 preguntas.
Sea la variable aleatoria discreta X,número de aciertos a preguntas dadas. Realizamos un resumen de los datos que nos ofrece el enunciado del problema:
La variable aleatoria discreta X, sigue una distribución binomial: X ~ B(200, 0.5).
Al ser preguntas de verdadero/falso, la probabilidad de acierto es de 0.5.
Comprobaremos, si se puede aproximar a la normal, para ello, se deben cumplir las siguientes condiciones:
1. n·p ≥ 5: 200·0.5 = 100 ≥ 5 OK.
2. n·q ≥ 5: 200·(1-0.5) = 100 ≥ 5 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
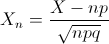
Por lo tanto: X ~ N(n·p, √(n·p·q)) = N(100, √50).
Pasamos a resolver los apartados dados.
Apartado a)
Debemos calcular: P(X ≤ 50), pero antes, debemos aplicar la corrección por continuidad, por lo tanto, tenemos: P(X ≤.50.5).
Tipificamos:
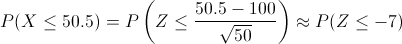
Operamos:
En las tablas de la Normal tipificada, se dispone del valor exacto en las tablas que están en Aqueronte para su consulta, por lo tanto: Φ(7) = 0.5.
Por lo tanto, la solución a este apartado es la siguiente:
Se puede concluir con el dato obtenido es que la probabilidad de que un individuo acierte menos o igual a cincuenta preguntas es nula, por lo tanto, se entiende que se acertarán más.
Apartado b)
Debemos calcular: P(50 < .X < .100), pero antes, debemos aplicar la corrección por continuidad, por lo tanto, tenemos: P(50.5 < .X < .99.5).
Tipificamos:

Simplificamos:
Simplificamos:
En las tablas de la Normal tipificada, se dispone del valor exacto en las tablas que están en Aqueronte para su consulta, por lo tanto:
· Φ(0.07) = 0.0279.
· Φ(7) = 0.5.
Por lo tanto, la solución a este apartado es la siguiente:
Apartado c)
Debemos calcular: P(X >.120) = 1 - P(X ≤ 120), pero antes, debemos aplicar la corrección por continuidad, por lo tanto, tenemos: 1 - P(X ≤.120.5).
Tipificamos:
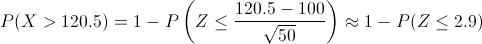
Operamos:
En las tablas de la Normal tipificada, se dispone del valor exacto en las tablas que están en Aqueronte para su consulta, por lo tanto:
· Φ(2.9) = 0.4981.
Por lo tanto, la solución a este apartado es la siguiente:
Por lo tanto, acertar más de 120 preguntas de un total de 200 es de 0.0019, una probabilidad baja.





5 comentarios:
Hola, en el apartado b, cuando se aplica la correccion por continuidad, en vez de 95.5 no se deberia aplicar 99,5?.
Fantastico su blog.
Un saludo.
Buenas:
Tienes toda la razón del mundo, ha sido un error al escribir la expresión que ido manteniendo a lo largo del apartado.
Aunque si te das cuenta, los cálculos están bien.
Un saludo y gracias por la corrección.
Disculpa pero por que en el operamos del apartado c) se usa P(x>120) y no 120.5 como la corrección por continuidad?
Buenas:
Si te fijas bien en el problema, se ha aplicado la corrección por continuidad, es más el propio inicio de la solución de dicho apartado lo menciona.
Un saludo.
Hola, en la C como calcularon de 2.9 a 0.4981
Publicar un comentario