Problema43: VAD

Ej43. Los mensajes que llegan a una computadora utilizada como servidor lo hacen de acuerdo con una distribución de Poisson con una tasa promedio de 0.1 mensajes por minuto.

Determinar:

a) ¿Cuál es la probabilidad de que lleguen como mucho 2 mensajes en una hora?.

b) Determinar el intervalo de tiempo necesario para que la probabilidad de que no llegue ningún mensaje durante ese lapso de tiempo sea de 0.8.


Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Número de mensajes que llegan a una computadora utilizada como servidor'.
· Tamaño de la muestra: n = 0.1 mensaje/minuto.
· La variable aleatoria X sigue una distribución Poisson: X ~ P(0.1).

Pasamos a resolver los apartados ofrecidos por el enunciado del problema.


Apartado a)

En este apartado, el entorno de estudio está expresado en horas, sabiendo que:

· 1 hora = 60 minutos-

Debemos adaptar nuestro parámetro promedio:

..0.1..--- 1
...λ....--- 60

Por lo tanto, el número medio de mensajes recibidos en la computadora es:

· λ = (60·0.1)/1 = 6

La probabilidad que debemos obtener es la siguiente:

P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)

Por lo tanto:

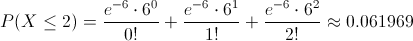
La probabilidad de que el ordenador reciba como máximo dos mensajes en una hora es de, aproximadamente, 0.061969.


Apartado b)

En este apartado deberemos obtener el tiempo en el que no llegue ningún mensaje a la computadora, teniendo en cuenta que dicha probabilidad es de 0.8.

P(X = 0) = 0.8

Sustituimos:

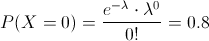
Empleamos las propiedades del logaritmo neperiano para despejar y resolver el parámetro promedio λ:

-λ = Ln(0.8)

Por lo tanto, el tiempo promedio es de, aproximadamente, λ ≈ 0.223144.

Lo pasamos a minutos:

......0.1........--- 1
0.223144...--- x

Por lo tanto, el tiempo en el que no llega ningún mensaje a la computadora teniendo en cuenta que la probabilidad para este hecho es de 0.8, es de, 0.223144/0.1 = 2.23144 minutos.