Ej44. El número de pinchazos en los neumáticos de cierto vehículo industrial tiene una distribución de Poisson con media 0.3 por cada 50000 kilómetros.
Si el vehiculo recorre 100000 km, se pide:
a) Probabilidad de que no tenga pinchazos.
b) Probabilidad de que tenga menos de tres pinchazos.
c) Número de km recorridos para que la probabilidad de que no tenga ningún pinchazo sea 0.4066.
Realizamos una recopilación de datos del enunciado del problema:
· X ≡ 'Número de pinchazos en los neumáticos de cierto vehículo industrial'.
· Tamaño de la muestra: n = 50000 km.
· La variable aleatoria X sigue una distribución Poisson: X ~ P(0.3).
Debemos adaptar nuestro parámetro promedio ya que el enunciado del problema trabaja en base a los 100000 km:
..0.3..--- .50000
...λ....--- 100000
Por lo tanto, el número medio de mensajes recibidos en la computadora es:
· λ = (100000·0.3)/50000 = 0.6
Pasamos a resolver los apartados ofrecidos por el enunciado del problema.
Apartado a)
La probabilidad que debemos obtener es la siguiente:
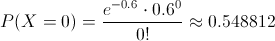
La probabilidad de no tener ningún pinchazo por cada 100000 km es de, aproximadamente, 0.548812.
Apartado b)
La probabilidad que debemos obtener es la siguiente:
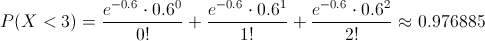
La probabilidad de tener menos de tres pinchazos por cada 100000 km es de, aproximadamente, 0.976885.
Apartado c)
En este apartado deberemos obtener los kilómetros necesarios para que el neumático no tenga ningún pinchazo, teniendo en cuenta que dicha probabilidad es de 0.4066.
Sustituimos:
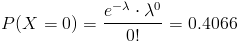
Empleamos las propiedades del logaritmo neperiano para despejar y resolver el parámetro promedio λ:
Por lo tanto, el tiempo promedio es de, aproximadamente, λ ≈ 0.899925.
Lo pasamos a kilómetros:
......0.3........--- 50000
0.899925...--- x
Por lo tanto, los kilómetros para que no tengan ningún pinchazo el neumático teniendo en cuenta que la probabilidad para este hecho es de 0.4066, es de, (0.899925·50000)/0.3 = 149987.5 km.





1 comentarios:
Hola buenas tardes la pregunta c esta mala dado que se debe tener de antemano la variable aleatoria el resultado interpretado de manera adecuada seria que el promedio de pinchazos es de 0.899925 pinchazos por cada 50000 km para que la probabilidad de to tener pinchazos sea 0.4966
Publicar un comentario