Problema48: VAC

Ej48. Los agricultores de una región están preocupados por la calidad de sus cosechas, ya que se ha detectado en ciertas áreas la existencia de sustancias contaminantes en el suelo.

Para analizarla, se segmenta la tierra en parcelas de 100 m², y se concluye que hay una probabilidad de 0.6 de encontrar estos contaminantes en una determinada parcela.

Una cooperativa posee 200 parcelas del tipo anterior. ¿Qué probabilidad hay de que tenga entre 100 y 150 parcelas contaminadas?. (ambas parcelas no incluidas)


Realizamos una recopilación de datos que nos ofrece el enunciado:

· Sea la variable aleatoria X, número de parcelas contaminadas.
· Tamaño de la muestra: N = 200 parcelas.
· La variable aleatoria discreta X sigue una distribución binomial: X ~ B(200, 0.6)

Comprobaremos, si se puede aproximar a la Normal, para ello, se deben cumplir las siguientes condiciones:

1. n·p ≥ 5 → 200·0.6 = 120 ≥ 5 OK.

2. n·q ≥ 5 → 200·(1-0.6) = 80 ≥ 5 OK.

Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:

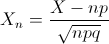
Por lo tanto: X ~ N(n·p, √(n·p·q)) = N(120, √48).

Debemos obtener la siguiente probabilidad:

P(100 < .X < .150)

Aplicamos el factor de corrección:

P(100.5 < .X < .149.5)

Y en estos momentos estamos en condiciones de tipificar por la Normal:

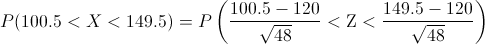
Aproximadamente es:

P(100.5 < .X < .149.5) ≈ P(-2.81 < .Z < .4.26)

Obtenemos:

P(100.5 < .X < .149.5) = (0.5 + Φ(4.26)) - [1 - (0.5 + Φ(2.81))] = Φ(4.26) + Φ(2.81)

Buscando en la tabla de la Normal, obtenemos la solución a este apartado:

P(100.5 < .X < .149.5) = Φ(4.26) + Φ(2.81) = 0.5 + 0.4975 = 0.9975

Por lo tanto, la probabilidad de que el número de parcelas contaminadas esté comprendidas entre 100 y 200, ambas no inclusive, de una muestra total de 200, es de 0.9975, una probabilidad bastante alta.