Problema49: VAD

Ej49. Una empresa electrónica observa que el número de componentes que fallan antes de cumplir 100 horas de funcionamiento es una variable aleatoria de Poisson. Si el número promedio de estos fallos es ocho.

Determinar:

a) ¿Cuál es la probabilidad de que falle un componente en 25 horas?

b) ¿Y de que fallen menos de dos componentes en 50 horas?

c) ¿Cuál es la probabilidad de que fallen por lo menos diez, en 125 horas?.


Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Nº de fallos de un componente en 100 horas de funcionamiento'.
· La variable aleatoria X sigue una distribución Poisson: X ~ P(8).

Pasamos a resolver los distintos apartados ofrecidos por el enunciado del problema.

Apartado a)

Debemos adaptar nuestro parámetro promedio ya que el estudio está basado en una jornada de 25 horas:

..100..--- 8
...25....--- λ

Por lo tanto, el número medio de fallos por componente (de 25 horas) es:

· λ = (8·25)/100 = 2

La probabilidad que debemos obtener es la siguiente:

Por lo tanto, la probabilidad de que un componente falle en 25 horas, es de, aproximadamente, 0.270671.


Apartado b)

Debemos adaptar nuestro parámetro promedio ya que el estudio está basado en una jornada de 50 horas:

..100..--- 8
...50....--- λ

Por lo tanto, el número medio de fallos por componente (de 50 horas) es:

· λ = (8·50)/100 = 4

La probabilidad que debemos obtener es la siguiente:

P(X < .2) = P(X = 0) + P(X = 1)

Sustituimos:

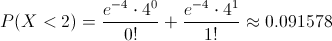
Por lo tanto, la probabilidad de que menos de dos componentes fallen en 50 horas, es de, aproximadamente, 0.091578.


Apartado c)

Debemos adaptar nuestro parámetro promedio ya que el estudio está basado en una jornada de 125 horas:

..100..--- 8
..125....--- λ

Por lo tanto, el número medio de fallos por componente (de 125 horas) es:

· λ = (8·125)/100 = 10

La probabilidad que debemos obtener es la siguiente:

P(X ≥ 10) = 1 - P(X < .10) = 1 - [P(X = 0) + ··· + P(X = 9)]

Para este apartado, emplearemos el software R para obtener la solución final:

> ppois(c(10), 10, lower.tail = F)
[1] 0.4169602

Por lo tanto, la probabilidad de que al menos diez componentes fallen en 125 horas, es de, aproximadamente, 0.416960.