Problema55: VAC

Ej55. Se ha comprobado que el tiempo de vida de cierto tipo de marcapasos sigue una distribución exponencial con media de 16 años.

Determinar:

a) ¿Cuál es la probabilidad de que a una persona a la que se le ha implantado este marcapasos se le deba reimplantar otro antes de 20 años?

b) Si el marcapasos lleva funcionando correctamente 5 años en un paciente, ¿cuál es la probabilidad de que haya que cambiarlo antes de 25 años?


Realizamos una recopilación de datos que nos ofrece el problema:

· X ≡ 'Tiempo de vida de cierto tipo de marcapasos'.
· La variable X se distribuye de forma exponencial: X ~ exp(16) años.

Pasamos a resolver los apartados ofrecidos por el enunciado del problema.


Apartado a)

En este apartado, debemos obtener la siguiente probabilidad:

P(X < .20)

Para resolverlo, emplearemos la distribución acumulada sabiendo que la función de densidad de probabilidad de la distribución exponencial es:

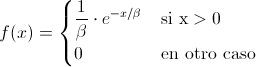
Siendo:

· β = 16.

Y que la relación entre función de densidad de probabilidad y función de distribución acumulada es:

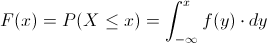
Por lo tanto:

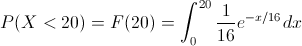
Realizamos el siguiente cambio de variable:

· t = -x/16
· dt = -dx/16

Sustituimos:

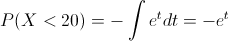
Deshacemos el cambio de variable:

· t = -x/16

Sustituimos y obtenemos la solución a este apartado:

P(X < .20) = -e^-x/16|²⁰₀ = -(e^-20/16 - 1) = 1 - e^-5/4 ≈ 0.713495

Por lo tanto, la probabilidad de que el tiempo de vida de este tipo de marcapasos sea inferior a 20 años es de, aproximadamente, 0.713495.


Apartado b)

En este apartado debemos obtener la siguiente probabilidad:

P(X < .20+5| X > 5)

Hay que tener en cuenta que una de las propiedades fundamentales de la distribución exponencial es que carece de memoria, por lo tanto:

P(X < .20+5| X > 5) = P(X < .20)

En este apartado se demuestra, parcialmente, de la propiedad de la carencia de memoria, ya que la probabilidad que se debe obtener ya se ha hallado en el apartado anterior.

Por lo tanto, la solución a este apartado es, aproximadamente, 0.713495.