Problema54: VAC

Ej54. En un experimento de laboratorio se utiliza cierto material. Sabiendo que la duración media de un átomo de esta materia es de 140 días y que sigue una distribución exponencial, ¿cuántos días transcurrirán hasta que haya desaparecido el 90% de este material?.


Realizamos una recopilación de datos que nos ofrece el problema:

· X ≡ 'Tiempo transcurrido hasta que desaparezca el material'.
· La variable X se distribuye de forma exponencial: X ~ exp(140) días.

En este problema, debemos obtener los días que transcurren hasta que desaparezca el material dada una probabilidad:

P(X ≤ R) = 0.9

Para resolverlo, emplearemos la distribución acumulada sabiendo que la función de densidad de probabilidad de la distribución exponencial es:

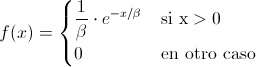
Siendo:

· β = 140.

Y que la relación entre función de densidad de probabilidad y función de distribución acumulada es:

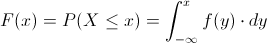
Por lo tanto:

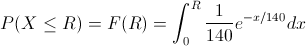
Realizamos el siguiente cambio de variable:

· t = -x/140
· dt = -dx/140

Sustituimos:

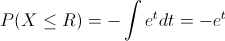
Deshacemos el cambio de variable:

· t = -x/140

Sustituimos y obtenemos la solución a este apartado:

P(X ≤ R) = -e^-x/140|^R₀ = -(e^-R/140 - 1) = 1 - e^-R/140

Empleamos la función de distribución acumulada obtenida:

P(X ≤ R) = F(R) = 1 - e^-R/140 = 0.9

Simplificamos:

e^-R/140 = 0.1

Empleamos las propiedades del logaritmo neperiano para resolver este apartado:

-R/140 = Ln(0.1)

Despejamos el parámetro R para obtener la solución:

R = -140·Ln(0.1) = 322.361913

Por lo tanto, el tiempo transcurrido hasta que desaparezca el material dada una probabilidad de 0.9 es de, 322.361913 días.