Ej53. Una fábrica produce en cada turno 100000 bolas para rodamientos de forma que la probabilidad de defectuosa es 0.04. En el control de las bolas se revisan todas depositando las defectuosas (que se detectan todas) en un recipiente que se vacía al final de cada turno.
¿Cuántas bolas ha de contener el recipiente para que la probabilidad de que su capacidad no se vea rebasada, sea 0.95?.
Sea la variable aleatoria discreta X, número de bolas que contiene el recipiente. Realizamos en resumen de los datos que nos ofrece el enunciado del problema:
La variable aleatoria discreta X, sigue una distribución binomial: X ~ B(100000, 0.04).
Comprobaremos, si se puede aproximar a la Normal, para ello, se deben cumplir las siguientes condiciones:
1. n·p ≥ 5 → 100000·0.04 = 4000 ≥ 5 OK.
2. n·q ≥ 5 → 100000·(1-0.04) = 3840 ≥ 5 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
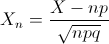
Por lo tanto: X ~ N(n·p, √(n·p·q)) ≈ N(4000, 61.967734).
En este problema, debemos obtener la cantidad de bolas que contiene el recipiente para una probabilidad dada.
Y en estos momentos estamos en condiciones de tipificar por la Normal:
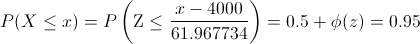
Despejamos Φ(z):
Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:
..1.64.............Z..........1.65
0.4495........0.45.....0.4505
De donde:
1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z..-> 0.4495 - 0.45
Calculamos:
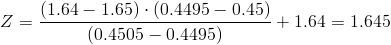
Por lo tanto, tenemos:
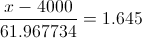
Despejamos la variable a determinar, para obtener la solución a este apartado:
Por lo tanto y teniendo en cuenta que las bolas deben ser unidades enteras, el valor total de bolas que ha de contener el recipiente para que la probabilidad de su capacidad no se vea rebosada de 0.95, es de, aproximadamente, 4102 bolas.





0 comentarios:
Publicar un comentario