Problema52: VAC

Ej52. El peso de las naranjas de un determinado calibre, fluctúa normalmente con media 150 gr, y desviación típica 30 gr. Si una bolsa se llena con 15 naranjas seleccionadas al azar.

¿Cuál es la probabilidad de que el peso total de la bolsa sea inferior a 2 kilos?.


Realizamos una recopilación de datos que nos ofrece el problema:

· X ≡ 'Peso de las naranjas de un determinado calibre'.

Dicha variable sigue una distribución normal:

· X ~ N(150, 30).

Hay que tener en cuenta que una bolsa consta de 15 naranjas, por lo que nuestra variable aleatoria se debe ajustar a dicha cantidad:

· X ~ N(150·15, 30·√15) = N(2250, 30·√15).

Debemos obtener la siguiente probabilidad:

P(X < .2000)

Tipificamos:

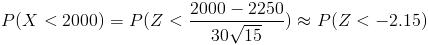
Manipulamos la expresión:

P(X < .2000) = P(Z > 2.15) = 1 - P(Z ≤ 2.15)

Operamos:

P(X < .2000) = 1 - [0.5 + Φ(2.15)] = 0.5 - Φ(2.15)

Buscamos en las tablas de la Normal expuestas en este blog, para dar cómo resultado final:

P(X < .2000) = 0.5 - Φ(2.15) = 0.5 - 0.4842 = 0.0158

Por lo tanto, la probabilidad de que en una bolsa de 15 naranjas, el peso total de ésta es inferior a 2 kg es de, aproximadamente, 0.0158.