Problema51: VAC

Ej51. El personal de la compañía Onda S.L. usa una Terminal para realizar sus pedidos internacionales. Si el tiempo que cada comercial gasta en una sesión en la Terminal tiene una distribución exponencial con media 36 minutos, encontrar:

a) Probabilidad de que un comercial utilice la Terminal 30 minutos o menos.

b) Si un comercial a estado 30 minutos en la Terminal, ¿Cuál es la probabilidad de que pase al menos una hora más en la Terminal?.

c) El 90% de las sesiones terminan en menos de R minutos. ¿Cuánto vale R?.


Realizamos una recopilación de datos que nos ofrece el problema:

· X ≡ 'Tiempo que cada comercial gasta en una sesión en la Terminal'.
· La variable X se distribuye de forma exponencial: X ~ exp(36) minutos

Pasamos a resolver los distintos apartados ofrecidos.


Apartado a)

Debemos obtener la siguiente probabilidad:

P(X ≤ 30)

Para resolver este apartado, emplearemos la distribución acumulada sabiendo que la función de densidad de probabilidad de la distribución exponencial es:

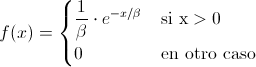
Siendo:

· β = 36.

Y que la relación entre función de densidad de probabilidad y función de distribución acumulada es:

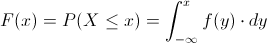
Por lo tanto:

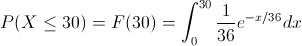
Realizamos el siguiente cambio de variable:

· t = -x/36
· dt = -dx/36

Sustituimos:

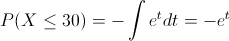
Deshacemos el cambio de variable:

· t = -x/36

Sustituimos y obtenemos la solución a este apartado:

P(X ≤ 30) = -e^-x/36|³⁰₀ = -(e^-30/36 - 1) = 1 - e^-30/36 ≈ 0.565402

Por lo tanto, la probabilidad de que un comercial emplee el Terminal 30 minutos o menos es de, aproximadamente, 0.565402.


Apartado b)

En este apartado debemos obtener la siguiente probabilidad:

P(X ≥ 30+60| X ≥ 30)

Hay que tener en cuenta que una de las propiedades fundamentales de la distribución exponencial es que carece de memoria, por lo tanto:

P(X ≥ 30+60| X ≥ 30) = P(X ≥ 60) = 1 - P(X < .60)

Para resolver este apartado empleamos la función de distribución acumulada obtenida en el apartado anterior pero esta vez, para un límite de 60:

P(X ≥ 60) = 1 - P(X < .60) = 1 - [1 - e^-60/36] = e^-60/36 ≈ 0.188876

Por lo tanto, la probabilidad de dado que comercial haya estado usando el Terminal 30 minutos, la probabilidad de que pase al menos una hora o más en el Terminal es de, aproximadamente, 0.188876.


Apartado c)

En este apartado, debemos obtener el tiempo usando el Terminal un comercial dada una probabilidad:

P(X < .R) = 0.9

Empleamos la función de distribución acumulada obtenida en el primer apartado con límite R:

P(X < .R) = F(R) = 1 - e^-R/36 = 0.9

Simplificamos:

e^-R/36 = 0.1

Empleamos las propiedades del logaritmo neperiano para resolver este apartado:

-R/36 = Ln(0.1)

Despejamos el parámetro R para obtener la solución:

R = -36·Ln(0.1) ≈ 82.893063

Por lo tanto, el tiempo empleado por el comercial en el Terminal dada una probabilidad de 0.9 es de, aproximadamente, 82.893063 minutos.