Problema50: VAC

Ej50. Supóngase que la concentración que cierto contaminante se encuentra distribuida de manera uniforme en el intervalo de 0 a 20 pares de millón. Si se considera tóxica una concentración de 8 o más.

Determinar:

a) ¿Cuál es la probabilidad de que al tomarse una muestra la concentración de esta sea tóxica?.

b) Concentración media y varianza.

c) Probabilidad de que la concentración sea exactamente 10.


Realizamos una recopilación de datos que nos ofrece el problema:

· X ≡ 'Concentración de cierto contaminante'.
· T ≡ 'Sea tóxica'. T ≥ 8.
· La variable X se distribuye de forma uniforme: X ~ U(0, 20)

Pasamos a resolver los distintos apartados ofrecidos.


Apartado a)

Debemos obtener la siguiente probabilidad:

P(X ≥ 8) = 1 - P(X < .8)

Empleamos la función de distribución acumulada de la distribución uniforme:

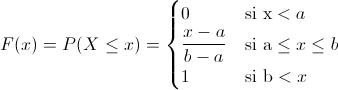
La solución a este apartado es la siguiente:

P(X ≥ 8) = 1 - P(X < .8) = 1 - (8-0)/(20-0) = 1 - 2/5 = 3/5

Por lo tanto, la probabilidad de que al tomarse una muestra ésta, sea tóxica es de 0.6.


Apartado b)

En este apartado debemos obtener el valor de la media y la varianza, empleamos para tal fin, sus expresiones matemáticas.

La media de la distribución uniforme viene dada por:

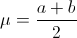
Por lo tanto, el valor de la media es:

μ = (0+20)/2 = 10

Esto quiere decir que la concentración media en ppm es de 10.

Y la varianza de la distribución uniforme viene expresada por:

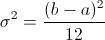
Sustituimos valores para obtener la varianza:

σ² = (20-0)²/2 = 100/3

Esto quiere decir que la varianza de concentración en ppm es de, aproximadamente, 33.333333.


Apartado c)

En este apartado, debemos obtener la siguiente probabilidad:

P(X = 10)

Al ser una distribución continua, lo que estamos obteniendo, matemáticamente hablando, es el área que encierra la curva de la distribución acumulada en un intervalo dado.

En este caso, la probabilidad que nos piden obtener no se encuentra en ningún intervalo, sino que es un dato discreto, por lo tanto, el área es nula.

Esto quiere decir que, la solución a este problema es:

P(X = 10) = 0

En las distribuciones continuas, los valores discretos no contienen ningún área y por ende, su valor es cero.