Problema56: VAC

Ej56. Supongamos que el cuerpo de bomberos de una gran ciudad es capaz de atender hasta un máximo de 300 servicios por día. Si el numero medio de servicios diarios es de 250 con distribución de Poisson, determinar:

¿Cuál es la probabilidad de que un día determinado no se puedan atender todos los servicios requeridos?


Realizamos una recopilación de datos que nos ofrece el enunciado:

· Sea la variable aleatoria X, número de servicios que son capaces de atender un cuerpo de bomberos.
· La variable aleatoria discreta X sigue una distribución Poisson: X ~ P(250)
· El cuerpo de bomberos puede atender hasta 300 servicios al día como máximo.

Debemos obtener la siguiente probabilidad:

P(X > 300) = 1 - P(X ≤ 300)

Comprobaremos, si se puede aproximar a la Normal, para ello, se deben cumplir la siguiente condición:

1. λ > 25 → 250 > 25 OK.

Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:

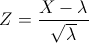
Por lo tanto: X ~ N(λ, √λ) = N(250, √250).

Aplicamos el factor de corrección:

P(X > 300) = 1 - P(X ≤ 300.5)

Y en estos momentos estamos en condiciones de tipificar por la Normal:

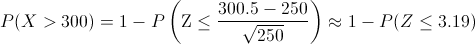
Obtenemos:

P(X > 300) = 1 - P(Z ≤ 3.19) = 1 - [0.5 + Φ(3.19)] = 0.5 - Φ(3.19)

Buscando en la tabla de la Normal, obtenemos la solución a este apartado:

P(X > 300) = 0.5 - Φ(3.19) = 0.5 - 0.4993 = 0.0007

Por lo tanto, la probabilidad de que el servicio de bomberos de dicha gran ciudad, no sea capaz de cumplir todos los servicios en un día, es de 0.0007, como podemos observar, una probabilidad bastante baja.