Ej57. Supongamos que el consumo familiar de un cierto producto se distribuye como una variable aleatoria de distribución uniforme, con esperanza igual a 10 y varianza unidad.
Determina la probabilidad de que dicho consumo este comprendido entre 8 y 12 unidades.
Realizamos una recopilación de datos que nos ofrece el problema:
· X ≡ 'Consumo familiar de cierto producto'.
· La variable X se distribuye de forma uniforme: X ~ U(a, b)
Para resolver la probabilidad requerida, previamente debemos obtener los valores de los límites de la distribución uniforme, y para tal fin, emplearemos los datos que nos ofrecen sobre la media y la varianza de dicha distribución.
La media de la distribución uniforme viene dada por:
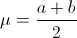
Teniendo en cuenta el valor dado de la media:
Obtenemos la primera ecuación: a+b = 20
Y la varianza de la distribución uniforme viene expresada por:
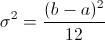
Teniendo en cuenta el valor de la varianza:
Obtenemos la segunda ecuación: b-a = √12
Resumiendo, tenemos dos ecuaciones con dos incógnitas, por lo tanto, los valores de las variables son:
· a = 10-√3 ≈ 8.267949.
· b = 10+√3 ≈ 11.732051.
Una vez obtenidos los límites de la distribución uniforme, la probabilidad que debemos determinar es la siguiente:
Podemos observar que el límite superior (b) es inferior al límite de la probabilidad dada: 12 > b, por lo que la solución a la probabilidad dada es, 1.





2 comentarios:
Hola Manuel:
Soy Renata de nuevo,consultandote sobre el ejercicio 57, primeramente gracias por contestarme, luego quiero consultarte otra duda que tengo respecto a los pasos que me explicastes para obtener el valor √3, al momento de despejar :
Despejamos:
· a = 20/2 - √[12/4] = 10 - √3
Tengo dudas de donde se tomo el 4 que esta dividiendo el 12 ,√[12/4] ? Otra consulta que te quiero hacer es que en el problema que estoy resolviendo que es similar al problema 57 que tu planteas en el blog, sin embargo en el ejercicio que tengo que resolver solo me da la media y la varianza, y se me pide encontrar los valores de a y b, en el ejercicio no se me proporciona un rango de probabilidad,ya que la media que me esta dando es igual a 2, estoy asumiendo tomar un rango de probabilidad entre 1 y 3. A tu criterio es correcto que tome ese rango? Disculpa la insistencia con este mismo problema, pero deseo entender el problema al 100%. Agradezco tu comprension y apoyo.
Renata
Buenas Renata:
Te lo puse en el mensaje anterior, te muestro todos los pasos:
· a = 20/2 - (√12)/2 = 10 - √[12/4] = 10 - √3
Fíjate que el 2 que está dividiendo entra en la raíz elevado al cuadrado.
Con respecto a tu problema, si sólo tienes que obtener los límites (a y b) de la distribución uniforme y te dan como datos la media y varianza, no necesitas asumir ningún intervalo de probabilidad.
Con las expresiones matemáticas de la media y varianza de la distribución uniforme, tienes dos ecuaciones con dos incógnitas, dónde podrás obtener los valores de a y b.
En este problema se pide ambos parámetros: a y b, y después, se pide que se obtenga una probabilidad, pero ésto es otro apartado distinto, no es necesario para la obtención de los límites a y b.
· PD: No repetir el mismo mensaje en diferentes partes del blog.
Un saludo y gracias por tu comentario.
Publicar un comentario