Problema56: Probabilidad

Ej56. Dos maquinas A y B han producido respectivamente, 100 y 200 piezas. Se sabe que A produce un 5% de piezas defectuosas y B un 6%.

Se toma una pieza y se pide:

a) Probabilidad de que sea defectuosa.

b) Sabiendo que es defectuosa, probabilidad de que proceda de la primera máquina.


Realizamos una recopilación de datos dados por el enunciado del problema:

· A ≡ 'Piezas fabricadas por la máquina A'.
· B ≡ 'Piezas fabricadas por la máquina B'.
· D ≡ 'Piezas defectuosas'.

· P(D|A) = 0.05.
· P(D|B) = 0.06.

Número de piezas fabricadas:
· Por la máquina A: 100
· Por la máquina B: 200

Número total de piezas: 100+200 = 300

Probabilidad de escoger una pieza:
· De la máquina A: P(A) = 100/300 = 1/3.
· De la máquina B: P(B) = 200/300 = 2/3.

Pasamos a resolver los apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de que la pieza seleccionada sea defectuosa, para ello, debemos emplear el teorema de la Probabilidad Total:

P(D) = P(D|A)·P(A) + P(D|B)·P(B) = 0.06·(1/3) + 0.06·(2/3) = 17/300

Por lo tanto, la probabilidad de que una pieza sea defectuosa, independientemente de la máquina de la que provenga, es de, aproximadamente 0.056667.


Apartado b)

En esta ocasión, debemos obtener la probabilidad de dada que la pieza es defectuosa, sea de la máquina A, para resolver este apartado, emplearemos la Ley de Bayes:

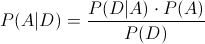
Sustituimos valores para obtener la solución:

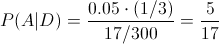
Por lo tanto, la probabilidad de dado que una pieza es defectuosa, sea de la máquina A es de, aproximadamente, 0.294118.