Ej57. El portero titular de un equipo de fútbol para 8 de cada 10 penaltis, mientras que el suplente solo para 5. El portero suplente juega, por termino medio, 15 minutos en cada partido (90 minutos).
Determinar:
a) Si en un partido se lanzan tres penaltis contra este equipo, ¿cuál es la probabilidad de que se paren los tres?
b) Si se lanza un penalti y no se para ¿cuál es la probabilidad de que estuviera jugando el portero titular?:
Realizamos una recopilación de datos dados por el enunciado del problema:
· E ≡ 'Tiempo que juega el portero titular'.
· A ≡ 'Parar un penalti'.
· P(A|E) = 8/10 = 4/5.
· P(A|Ē) = 5/10 = 1/2.
Tiempo de juego de cada portero:
· Portero suplente: P(Ē) = 15/90 = 1/6.
· Portero titular: P(E) = 1 - 1/6 = 5/6.
Pasamos a resolver los apartados que nos propone el enunciado del problema.
Apartado a)
En este apartado nos piden hallar la probabilidad de que se paren tres penaltis seguidos, para ello, debemos emplear el teorema de la Probabilidad Total, para obtener la probabilidad de parar un penalti.
Pasamos a obtener dicha probabilidad:
Pero en este problema nos piden la probabilidad de parar tres penaltis seguidos, teniendo en cuenta que los sucesos de parar un penalti son independientes, tenemos:
Por lo tanto, la probabilidad de parar tres penaltis consecutivos, independientemente del portero que juegue el partido, es de 0.421875.
Apartado b)
En esta ocasión, debemos obtener la probabilidad de dado que el penalti no se pare, esté jugando el portero titular, para resolver este apartado, emplearemos la Ley de Bayes:
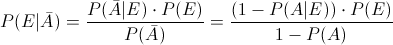
Sustituimos valores para obtener la solución:
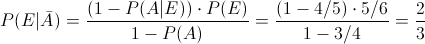
Por lo tanto, la probabilidad de dado que esté jugando el portero titular, el penalti no se pare es de, aproximadamente, 0.666667.





0 comentarios:
Publicar un comentario