Ej58. En un colegio hay dos grupos de 25 alumnos de quinto curso y dos grupos de 20 alumnos de sexto curso. El 50 % de los alumnos de quinto no tienen faltas de ortografía, porcentaje que sube a 70% en los alumnos de sexto.
En un concurso de redacción entre alumnos de quinto y sexto se elige una redacción al azar, determinar:
a) ¿Qué probabilidad hay de que sea de un alumno de quinto?
b) Si tiene faltas de ortografía, ¿qué probabilidad hay de que sea de un alumno de quinto?
Realizamos una recopilación de datos dados por el enunciado del problema:
· A ≡ 'Ser alumno de 5º curso'.
· B ≡ 'Ser alumno de 6º curso'.
Existen dos grupos en cada curso:
· De 5ºCurso: Dos grupos de 25 alumnos: TOTAL = 25+25 = 50 alumnos 5ºCurso.
· De 6ºCurso: Dos grupos de 20 alumnos: TOTAL = 20+20 = 40 alumnos 6ºCurso.
El número total de alumnos es: 50+40 = 90 alumnos.
· P(A) = 50/90 = 5/9.
· P(B) = 40/90 = 4/9.
· E ≡ 'Tener faltas de ortografía'.
· P(Ē|A) = 0.5.
· P(Ē|B) = 0.7.
Pasamos a resolver los apartados que nos propone el enunciado del problema.
Apartado a)
En este apartado nos piden la probabilidad de que la redacción escogida sea de un alumno de 5º Curso, ésta probabilidad ya ha sido calculado en el estudio previo:
Por lo tanto, la probabilidad de escoger una redacción al azar y ser ésta de un alumno de quinto es de, aproximadamente, 0.555556.
Apartado b)
En esta ocasión, debemos obtener la probabilidad de dado que tenga faltas de ortografía, ésta sea de un alumno de 5ºCurso, para resolver este apartado, emplearemos la Ley de Bayes:
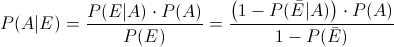
Obtenemos previamente, la probabilidad de no tener faltas de ortografía, para tal fin, empleamos la la relación de Probabilidad Total:
Sustituimos valores para obtener la solución:
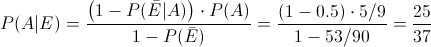





0 comentarios:
Publicar un comentario