Ej59. Una empresa que debe decidir si adquiere un determinado paquete de acciones, solicita un informe a tres asesores financieros para que se pronuncien de forma favorable o desfavorable a la compra.
Por experiencias anteriores en operaciones similares, se sabe que los tres asesores tienen actitudes ante el riesgo diferente e independiente. Esta situación se refleja en las probabilidades de aconsejar a compra de este tipo de operaciones que son respectivamente 0.8, 0.5 y 0.3.
Con esta información a priori, calcule:
a) La probabilidad de que al menos uno de ellos aconseje la compra.
b) La probabilidad de que ninguno de ellos aconseje adquirir el paquete de acciones.
Realizamos una recopilación de datos dados por el enunciado del problema:
· A ≡ 'Asesor 1 que aconseja la compra de acciones'.
· B ≡ 'Asesor 2 que aconseja la compra de acciones'.
· C ≡ 'Asesor 3 que aconseja la compra de acciones'.
· P(A) = 0.8.
· P(B) = 0.5.
· P(C) = 0.3.
Los eventos son independientes entre sí, por lo que dictamine un asesor no influye en la decisión de los demás.
Pasamos a resolver los apartados que nos propone el enunciado del problema.
Apartado a)
Debemos obtener la probabilidad de que alguno de los asesores aconseje la compra de acciones, tenemos:
Sustituimos valores, teniendo en cuenta que los sucesos son independientes entre sí, para obtener la solución a este apartado:
Por lo tanto, la probabilidad de alguno de los asesores recomiende la compra de acciones es de 0.93, en otras palabras, es bastante probable que alguno de ellos, recomienden la compra.
Apartado b)
En este apartado nos piden obtener la probabilidad de que ninguno te recomiende la compra de las acciones:
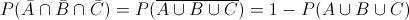
Sustituimos valores para obtener la solución de este apartado, empleando el dato del apartado anterior:
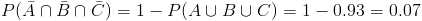
Por lo tanto, la probabilidad de ninguno de los asesores recomiende la compra de acciones es de 0.07.





0 comentarios:
Publicar un comentario