Problema60: Probabilidad

Ej60. Una empresa de trabajo temporal ha realizado un amplio estudio sobre los tipos de empleo solicitados por los estudiantes de Bachiller, Formación Profesional y Universitarios.

El informe clasifica estos solicitantes de empleo como cualificados o no para los trabajos que solicitan, y de los datos que contiene se desprende que sólo el 25% estaban cualificados para el trabajo que solicitaban, de los cuales, un 20% eran estudiantes universitarios, un 30% estudiaban Formación Profesional y un 50% Bachillerato.

La situación entre los no cualificados es diferente: un 40% de ellos era estudiante universitario, otro 40% estudiaban Formación Profesional y sólo un 20% se encontraba en Bachillerato.

Determinar:

a) ¿Qué probabilidad de estos estudiantes se encontraban en Bachillerato y estaban cualificados para los empleos que solicitaban?

b) ¿Cuál es la probabilidad de que uno de estos estudiantes que solicitaba empleo estudiara Formación Profesional?

c) Entre los estudiantes universitarios que solicitaron empleo, ¿qué porcentaje no estaba cualificado para los puestos de trabajo que solicitaban?


Realizamos una recopilación de datos dados por el enunciado del problema:

· U ≡ 'Estudiantes Universitarios'.
· B ≡ 'Estudiantes de Bachiller'.
· F ≡ 'Estudiantes de Formación Profesional'.
· E ≡ 'Solicitantes cualificados'.

· P(E) = 0.25.

· P(U|E) = 0.2.
· P(B|E) = 0.5.
· P(F|E) = 0.3.

· P(U|Ē) = 0.4.
· P(B|Ē) = 0.2.
· P(F|Ē) = 0.4.

Pasamos a resolver los apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de que el estudiante es de bachiller y la solicitud está cualificada:

P(B∩E) = P(B|E)·P(E) = 0.5·0.25 = 0.125

Por lo tanto, la probabilidad de ser estudiante de bachiller y la solicitud está cualificada, es de 0.125.


Apartado b)

En este apartado debemos obtener que uno de los mencionados estudiantes, estudiaran formación profesional, para tal fin, emplearemos la Probabilidad Total:

P(F) = P(F|E)·P(E) + P(F|Ē)·P(Ē) = 0.3·0.25 + 0.4·(1-0.25) = 0.375

Por lo tanto, la probabilidad de que uno de los mencionados estudiantes que solicitan empleo, estudie formación profesional es de 0.375.


Apartado c)

En esta ocasión, debemos obtener la probabilidad de dado que la solicitud de empleo sea de un estudiante universitario, ésta sea no cualificada, para resolver este apartado, emplearemos la Ley de Bayes:

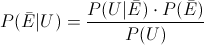
Primero, debemos obtener que uno de los mencionados estudiantes fuera universitario, para tal fin, emplearemos la Probabilidad Total:

P(U) = P(U|E)·P(E) + P(U|Ē)·P(Ē) = 0.2·0.25 + 0.4·(1-0.25) = 0.35

Sustituimos valores para obtener la solución:

Por lo tanto, la probabilidad de dado sea un estudiante universitario solicite el empleo, ésta sea no cualificada es de, aproximadamente, 0.857143.