Problema61: Probabilidad

Ej61. En un sistema de alarma, la probabilidad de que esta funcione habiendo peligro es 0.95 y la de que funcione por error sin haber peligro es 0.03.

Si la probabilidad de haber peligro es 0.1, determinar:

a) Calcular la probabilidad que habiendo funcionado la alarma no haya peligro.

b) Hallar la probabilidad de que haya peligro y la alarma no funcione.

c) Calcular la probabilidad de que no habiendo funcionado la alarma haya peligro.

d) ¿Cuál es la probabilidad de que la alarma funcione?


Realizamos una recopilación de datos dados por el enunciado del problema:

· O ≡ 'Alarma funciona'.
· E ≡ 'Peligro'.

· P(E) = 0.1.

· P(O|E) = 0.95.
· P(O|Ē) = 0.03.

Pasamos a resolver los apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de que dado que funcione la alarma, no exista riesgo de peligro:

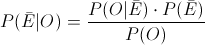
Primero, debemos obtener que la alarma funcione, para tal fin, emplearemos la Probabilidad Total:

P(O) = P(O|E)·P(E) + P(O|Ē)·P(Ē) = 0.95·0.1 + 0.03·(1-0.1) = 0.122

Sustituimos valores para obtener la solución:

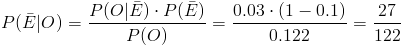
Por lo tanto, la probabilidad de que la alarma funcione sin que exista peligro es de, aproximadamente, 0.221311.


Apartado b)

En este apartado nos piden obtener la probabilidad de que exista peligro y la alarma no funcione:

P(E∩Ō) = P(Ō|E)·P(E) = [1-P(O|E)]·P(E) = [1-0.95]·0.1 = 0.005

Por lo tanto, la probabilidad de que exista peligro y la alarma no funcione, es de 0.005, en otras palabras, este caso es poco probable que ocurra.


Apartado c)

En este apartado debemos obtener que uno de los mencionados estudiantes, estudiaran formación profesional, para tal fin, emplearemos la Probabilidad Total:

P(F) = P(F|E)·P(E) + P(F|Ē)·P(Ē) = 0.3·0.25 + 0.4·(1-0.25) = 0.375

Por lo tanto, la probabilidad de que uno de los mencionados estudiantes que solicitan empleo, estudie formación profesional es de 0.375.


Apartado c)

En este apartado nos piden obtener la probabilidad de que dado que no funcione la alarma, exista riesgo de peligro:

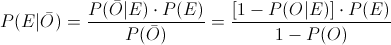
Sustituimos valores y obtenemos la solución a este apartado:

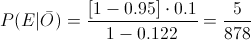
Por lo tanto, la probabilidad de que dada que la alarma no funcione, exista peligro es de, aproximadamente, 0.005695, una probabilidad baja.


Apartado c)

Este apartado está resuelto en el primer apartado:

P(O) = P(O|E)·P(E) + P(O|Ē)·P(Ē) = 0.95·0.1 + 0.03·(1-0.1) = 0.122

La probabilidad de que la alarma funcione es de 0.122.