Ej62. Una empresa multinacional desea elegir un candidato para ocupar la plaza de director técnico de la delegación que va a abrir en España. Tras las tres primeras pruebas de selección de los 100 candidatos iniciales, tres han quedado para la cuarta y última prueba que consistirá en una entrevista personal.
A la vista de los currículums presentados y de las puntuaciones obtenidas en las pruebas anteriores, se cuenta con probabilidades 0.3, 0.5 y 0.2 de elegir para el puesto a los candidatos 1º, 2º, y 3º respectivamente.
Se estima en un 80% las posibilidades de incrementar las ventas en el próximo año en la multinacional, si se elige al primer candidato. Para los otros dos: 2º y 3º, respectivamente se estiman el 10% y el 40% de posibilidades.
¿Qué candidato es el más idóneo para el puesto?
Realizamos una recopilación de datos dados por el enunciado del problema:
· A ≡ 'Candidato 1º'.
· B ≡ 'Candidato 2º'.
· C ≡ 'Candidato 3º'.
· P(A) = 0.3.
· P(B) = 0.5.
· P(C) = 0.2.
· I ≡ 'Incrementar las ventas'.
· P(I|A) = 0.8.
· P(I|B) = 0.1.
· P(I|C) = 0.4.
El candidato más idóneo para ser contratado es aquel cuya probabilidad sea mayor dado que van a aumentar las ventas gracias a su contratación.
· Para el candidato 1º:
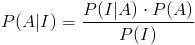
· Para el candidato 2º:
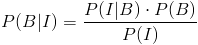
· Para el candidato 3º:
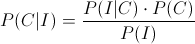
Primero, debemos obtener la probabilidad de aumentar las ventas, para tal fin, emplearemos la Probabilidad Total:
Sustituimos valores para cada candidato:
· Para el candidato 1º:
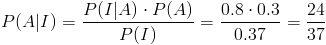
Por lo tanto, la probabilidad dado que se incrementan las ventas, escoger al candidato 1º es de, aproximadamente 0.648649.
· Para el candidato 2º:
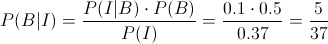
Por lo tanto, la probabilidad dado que se incrementan las ventas, escoger al candidato 2º es de, aproximadamente 0.135135.
· Para el candidato 3º:
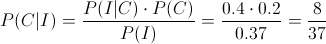
Por lo tanto, la probabilidad dado que se incrementan las ventas, escoger al candidato 3º es de, aproximadamente 0.216216.
Se puede observar, que el candidato más idóneo dada que se incrementan las ventas, es el 1º candidato.





0 comentarios:
Publicar un comentario