Ej67. En una universidad en la que solo hay estudiantes de arquitectura, Ciencias y Letras, terminan la carrera el 5% de arquitectura, el 10% de Ciencias y el 20% de Letras.
Se sabe que el 20% estudian arquitectura, el 30% Ciencias y el 50% Letras. Eligiendo un estudiante al azar, se pide:
a) Probabilidad de que sea de arquitectura y que haya terminado la carrera.
b) Nos dice que ha terminado la carrera. Probabilidad de que sea de Arquitectura.
Realizamos una recopilación de datos dados por el enunciado del problema:
· A ≡ 'Estudiante de arquitectura'.
· C ≡ 'Estudiante de ciencias'.
· L ≡ 'Estudiante de letras'.
· P(A) = 0.2.
· P(C) = 0.3.
· P(L) = 0.5.
· T ≡ 'Terminar la carrera'.
· P(T|A) = 0.05.
· P(T|C) = 0.1.
· P(T|L) = 0.2.
Pasamos a resolver los apartados que nos propone el enunciado del problema.
Apartado a)
En este apartado nos piden obtener la probabilidad de que el estudiante sea de arquitectura y acabe la carrera:
Por lo tanto, la probabilidad de estudiar arquitectura y acabar la carrera es de 0.01.
Apartado b)
En este apartado nos piden obtener la probabilidad de que dado que el estudiante acabe la carrera, sea de arquitectura:
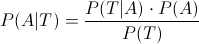
Antes, debemos obtener la probabilidad de acabar la carrera, para ello, empleamos la Probabilidad Total:
Sustituimos valores:
Sustituimos valores para obtener la solución a este apartado:
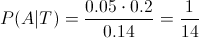
Por lo tanto, la probabilidad de dado que se acabe la carrera, sea un estudiante de arquitectura es de, aproximadamente 0.071429.





10 comentarios:
hola estuve viendo tu blog y estoy entrampada en una tontería en bioestadística.¿me podrías ayudar??
mi correo es alejandra.sotogrez@gmail.com
el asunto es que me piden la probabilidad siguiente:
p(-1.31 < t 30< 2.04)
y no sé cómo calcularla.
Buenas Alejandra:
¿Realmente es esa la probabilidad que quieres obtener? La notación es más que sospechosa.
Supongo que al haber una t, significa que la distribución a dicha probabilidad es la t-Student, pero el 30 me desconcierta, aunque puedo entenderlo como los grados de libertad necesarios.
Pero aún así, faltaría el valor de área de cola, α.
Es decir, si interpretamos que es una distribución t-Student, tenemos que obtener:
· P(-1.31 < T < 2.04)= Φ(2.04)-(-Φ(1.31)) = Φ(2.04)+Φ(1.31)
Como datos, tenemos los grados de libertad que serían 30, pero verás, que nos falta el área de cola.
En fin, con los datos que me proporcionas no puedo serte de mucha ayuda.
Un saludo y gracias por tu comentario.
AYUDA POR FAVOR:
CONSIGNAS:
(1) Un anagrama es una palabra que resulta de la transposición de letras de otra palabra. Cuantos anagramas (tengan o no significado) tiene la palabra GORILA, que:
1. Terminen con consonante
2. Comiencen con L y terminen con O
3. Comiencen con una vocal
4. Empiecen con una vocal y terminen con una consonante
5. Comiencen y terminen con consonante.
(2)
El dibujante de la historieta Mafalda dispone de 9 personajes diferentes para la tira, 5 varones y 4 mujeres, Quiere armar historietas con 2 varones y 2 mujeres. De cuántas formas puede formarse, si:
1. Puede pertenecer a la historieta cualquier varón o mujer.
2. Mafalda debe estar.
3. Dos varones determinados no pueden estar en la historieta.
(3) Se tiene una bolsa con nueve bolillas numeradas del 1 al 9. Se saca una bolilla de la bolsa se anota el número y se devuelve a la bolsa. Calcular las siguientes probabilidades y los porcentajes de probabilidad de que al sacar una bolilla:
a) sea un número par
b) sea un número primo
c) sea el cuadrado de un número.
d) sea menor que 10
e) sea un número menor que 5
f) sea un número menor que 1
(4) En una Universidad se pueden cursar tres carreras: Ingeniería, Ciencias y Letras. Se eligen 100 alumnos y resulta que 30 estudian Ingeniería, 45 estudian Ciencias y 25 Letras. Están por terminar la carrera de Ingeniería 18, de Ciencias 25 y de Letras 13. Tomando un estudiante al azar de ese grupo, se pide la probabilidad de que:
a) Sea de Ingeniería o Ciencias
b) Nos dicen que esta terminado la carrera, que probabilidad de que sea de ingeniería.
c) Nos dicen que es de ciencias, que probabilidad que no este terminado la carrera.
(5) Se lanza una moneda y si sale cara se ponen 7 bolas rojas en una bolsa y si sale cruz se ponen 4 rojas. Se vuelve a lanzar la moneda y se ponen 5 o 2 bolas azules, según se saque cara o cruz. Después se saca una bola de la bolsa así compuesta. Determinar:
a) la probabilidad de que sea roja
b) Si sabemos que la bola que ha salido es roja ¿cuál es la probabilidad de que hayan salido dos caras?
Armar el diagrama de árbol.
me podria ayudar
10. En una universidad el 70% de los estudiantes son del programa de ingeniería y el 30%
de letras; de los estudiantes de de Ingeniería el 60% son varones y los de letras son
varones el 40% Sise elige aleatoriamente un estudiante, calcular la probabilidad de que:
a) Sea un estudiante varón
b) Sea un estudiante mujer
c) Sea un estudiante varón si es de Ingeniería
d) Sea un estudiante de Letras si es mujer
e) Sea un estudiante de Letras y varón
11. Dos estudios contables A y B tienen 100 clientes cada uno, la proporción de que la
Sunat inspeccione a un cliente son 1/5 y 1/4 respectivamente. Se escoge un cliente al
azar
a) ¿Cuál es la probabilidad de que el cliente escogido viene del estudio contable A y
haya sido inspeccionado por Sunat?
b) Cuál es la probabilidad de que un cliente sea inspeccionado por Sunat, si proviene
del estudio contable B
12. Un cazador trata de matar a un oso La probabilidad que aparezca un oso en un radio
menor que R1 es de 0.5, en un radio entre R1 y R2 es de 0.3, y un radio mayor que R2
es 0.2 Si aparece un oso en un radio menor que R1, el cazador será capaz de matarlo con
una probabilidad de 0.7; con una probabilidad de 0.5 si aparece en un radio entre R1 y
R2; con una probabilidad de 0.2, si el radio es mayor de R2 ¿Cuál es la probabilidad de
que el cazador mate al oso?
5. Una Universidad reporta que 100 alumnos están inscritos en el curso de nuevo ingreso para la facultad de ciencia Económicas, dentro de las cuales 30% corresponden a la carrera de Licenciatura en Contaduría Pública, 45% a la Licenciatura en Mercadotecnia y el 25% a la Licenciatura en Administración de Empresa; De acuerdo a la ficha de registro el porcentaje de alumnos que aprueban dicho curso es de 60%, 90% y 40% respectivamente para cada una de las carreras. Eligiendo un alumno al azar, establezca la probabilidad que:
a) Apruebe el curso.
b) Apruebe, si se sabe que es de contabilidad.
c) No apruebe el curso.
d) No apruebe el curso, si se sabe que es de Administración.
AYUDA POR FAVOR CON ESTE EJERCICIO
Necesito que alguien me ayude con el ejercicio 5 que aparece sin resolver
5. Una Universidad reporta que 100 alumnos están inscritos en el curso de nuevo ingreso para la facultad de ciencia Económicas, dentro de las cuales 30% corresponden a la carrera de Licenciatura en Contaduría Pública, 45% a la Licenciatura en Mercadotecnia y el 25% a la Licenciatura en Administración de Empresa; De acuerdo a la ficha de registro el porcentaje de alumnos que aprueban dicho curso es de 60%, 90% y 40% respectivamente para cada una de las carreras. Eligiendo un alumno al azar, establezca la probabilidad que:
a) Apruebe el curso.
b) Apruebe, si se sabe que es de contabilidad.
c) No apruebe el curso.
d) No apruebe el curso, si se sabe que es de Administración.
Me ayudan con el ejercicio 5 que aparece sin resolver
Una Universidad reporta que 100 alumnos están inscritos en el curso de nuevo ingreso para la facultad de ciencia Económicas, dentro de las cuales 30% corresponden a la carrera de Licenciatura en Contaduría Pública, 45% a la Licenciatura en Mercadotecnia y el 25% a la Licenciatura en Administración de Empresa; De acuerdo a la ficha de registro el porcentaje de alumnos que aprueban dicho curso es de 60%, 90% y 40% respectivamente para cada una de las carreras. Eligiendo un alumno al azar, establezca la probabilidad que:
a) Apruebe el curso.
b) Apruebe, si se sabe que es de contabilidad.
c) No apruebe el curso.
d) No apruebe el curso, si se sabe que es de Administración.
Hola como resuelvo el siguiente problema
Una persona ha comprado 40 billetes de una lotería de 100 números. Si la lotería consta de tres premios. ¿Cuál es la probabilidad de que gane sólo un premio? ¿Al menos uno? ¿Ninguno?
Publicar un comentario