Ej80. En una facultad el 4% de los hombres y el 1% de las mujeres miden más de 1.75 m. de estatura. Además el 60% son mujeres.
Se elige un estudiante al azar y mide más de 1.75 m. de estatura, ¿cuál es la probabilidad de que sea mujer?.
Realizamos una recopilación de datos dados por el enunciado del problema:
· M ≡ 'Ser Mujer'.
· H ≡ 'Ser Hombre'.
· P(M) = 0.6.
· P(H) = 1 - P(M) = 1 - 0.6 = 0.4.
· A ≡ 'Medir más de 1.75 m'.
· P(A|M) = 0.01.
· P(A|H) = 0.04.
Nos piden obtener la probabilidad de que al escoger un alumno al azar y éste mide más de 1.75 m, que sea mujer.
Antes que nada, emplearemos la expresión de la probabilidad total, para obtener la probabilidad de medir más de 1.75 m.
P(A) = P(A|M)·P(M) + P(A|H)·P(H) = 0.01·0.6 + 0.04·0.4 = 0.022
Una vez obtenido dicho parámetro, pasamos a resolver el problema mediante la Ley de Bayes:
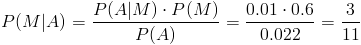
Por lo tanto, la probabilidad de que al escoger un alumno al azar y éste mide más de 1.75 m, sea mujer, es de, aproximadamente 0.272727.
1 comentarios:
No está bien el desarrollo, pues el problema se puede interpretar como que la probabilidad de que, al escoger un estudiante al azar, este sea hombre "Y" mida mas de 1.75 cm es de 0.04. Es la intersección de dos eventos, no es la probabilidad condicionada como dice el desarrollo. Esta interpretación es análoga para las mujeres
Publicar un comentario