Problema82: Probabilidad

Ej82. Las proporciones de piezas defectuosas fabricadas por dos máquinas M₁ y M₂ son 0.04 y 0.01, respectivamente. Se toma una pieza al azar y resulta aceptable.

Sabiendo que la probabilidad de elegir una pieza de cualquiera de las dos máquinas es 0.5, calcular la probabilidad de que provenga de M₁.


Realizamos una recopilación de datos dados por el enunciado del problema:

· M₁ ≡ 'Piezas fabricadas por la máquina 1'.
· M₂ ≡ 'Piezas fabricadas por la máquina 2'.

· P(M₁) = 0.5.
· P(M₂) = 0.5.

· D ≡ 'Pieza defectuosa'.

· P(D|M₁) = 0.04.
· P(D|M₂) = 0.01.

Nos piden obtener la probabilidad de que al escoger una pieza al azar y ésta no es defectuosa, que sea de la máquina 1.

Antes que nada, emplearemos la expresión de la probabilidad total, para obtener la probabilidad de pieza defectuosa.

P(D) = P(D|M₁)·P(M₁) + P(D|M₂)·P(M₂) = 0.04·0.5 + 0.01·0.5 = 0.025

Una vez obtenido dicho parámetro, pasamos a resolver el problema mediante la Ley de Bayes:

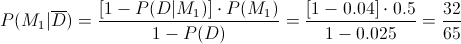
Por lo tanto, la probabilidad de que al escoger una pieza al azar y ésta no sea defectuosa, provenga de la máquina 1, es de, aproximadamente 0.492308.