Problema70: VAD

Ej70. Si la probabilidad de que un individuo sufra una reacción por una inyección de un determinado suero es 0.001, determinar la probabilidad de que de un total de 2000 individuos:

a) Exactamente 3 tengan reacción.

b) Más de 2 individuos tengan reacción.

Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Nº de individuos que sufren una reacción por inyección de un determinado suero'.
· La variable aleatoria X sigue una distribución Binomial: X ~ B(2000, 0.001).

Las características del tamaño de la muestra y la probabilidad relativamente baja que tiene, comprobaremos si podemos adaptar la distribución binomial a la de Poisson.

Para ello, debe cumplirse:

· n grande: n = 2000 OK.

· n·p = 2000·0.001 = 2 ≤ 7 OK.

Por lo tanto, se puede adaptar la variable aleatoria a la distribución de Poisson: X ~ P(2).

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)

Debemos obtener la siguiente probabilidad:

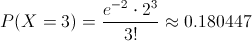
Por lo tanto, la probabilidad de que a tres individuos les haga reacción la inyección de un determinado suero es de, aproximadamente 0.180447.

Apartado b)

La probabilidad que debemos obtener es la siguiente:

P(X > 2) = 1 - P(X ≤ 2) = 1 - [P(X = 0) + P(X = 1) + P(X = 2)]

Al tener que calcularse el valor de varios elementos para obtener la solución a este apartado, vamos a emplear el software R para realizar dicha operación:

> 1 - ppois(2, 2)
[1] 0.3233236

Por lo tanto, la probabilidad de que a más de dos individuos les haga reacción la inyección de un determinado suero es de, aproximadamente 0.323324.