Problema83: Probabilidad

Ej83. Tres máquinas A, B y C producen piezas con una proporción de defectuosas del 5%, 3% y 2% respectivamente.

Se tiene un lote compuesto por 100 piezas de A, 50 de B y 50 de C. Se extrae una pieza al azar. Calcular:

a) Calcular la probabilidad de que la pieza sea defectuosa.

b) Si la pieza es defectuosa, calcular la probabilidad de que venga de A.


Realizamos una recopilación de datos dados por el enunciado del problema:

· A ≡ 'Pieza procedente de la máquina A'. Hay 100 piezas.
· B ≡ 'Pieza procedente de la máquina B'. Hay 50 piezas.
· C ≡ 'Pieza procedente de la máquina C'. Hay 50 piezas.

En total, existen: 100+50+50 = 200 piezas.

· P(A) = 100/200 = 0.5.
· P(B) = 50/200 = 0.25.
· P(C) = 50/200 = 0.25.

· D ≡ 'Pieza defectuosa'.

· P(D|A) = 0.05.
· P(D|B) = 0.03.
· P(D|C) = 0.02.

Pasamos a resolver los distintos apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden la probabilidad de obtener una pieza defectuosa, para tal fin, emplearemos la expresión de la probabilidad total.

P(D) = P(D|A)·P(A) + P(D|B)·P(B) + P(D|C)·P(C) = 0.05·0.5 + 0.03·0.25 + 0.02·0.25 = 0.0375

Por lo tanto, la probabilidad de obtener una pieza defectuosa es de 0.0375.


Apartado b)

En este apartado nos piden obtener la probabilidad de que dado que sea defectuosa la pieza, ésta provenga de la máquina A, emplearemos para tal fin la Ley de Bayes:

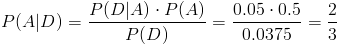
Por lo tanto, la probabilidad de que dado que sea defectuosa la pieza ésta, provenga de la máquina A es de, aproximadamente 0.666667.