Ej84. En un sistema protegido por una alarma, la probabilidad de que se produzca una situación de peligro es 0.1. Si éste se produce, la probabilidad de que la alarma funcione es 0.95.
La probabilidad de que la alarma funcione sin haber existido peligro es 0.03.
Hallar la probabilidad de que habiendo funcionado la alarma no haya habido peligro.
Realizamos una recopilación de datos dados por el enunciado del problema:
· E ≡ 'Hay peligro'.
· P(E) = 0.1.
· A ≡ 'Funciona la alarma'.
· P(A|E) = 0.95.
· P(A|Ē) = 0.03.
Nos piden obtener la probabilidad de que dada que la alarma funcione, no exista peligro.
Antes que nada, emplearemos la expresión de la probabilidad total, para obtener la probabilidad de que funcione la alarma.
P(A) = P(A|E)·P(E) + P(A|Ē)·P(Ē) = 0.95·0.1 + 0.03·(1-0.1) = 0.122
Una vez obtenido dicho parámetro, pasamos a resolver el problema mediante la Ley de Bayes:
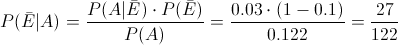
Por lo tanto, la probabilidad de que dada que la alarma funcione sin existir peligro, es de, aproximadamente 0.221311.
0 comentarios:
Publicar un comentario