Ej76. Suponga que una compañía de seguros vendió pólizas de seguros de vida a 5000 hombres de 42 años de edad. Si los estudios actuales indican que la probabilidad de que un hombre de 42 años muera en un determinado año es 0.001.
¿Cuál es la probabilidad de que la compañía pague 4 indemnizaciones en un determinado año?.
Realizamos una recopilación de datos del enunciado del problema:
· X ≡ 'Nº de indemnizaciones a pagar en un determinado año'.
· La variable aleatoria X sigue una distribución Binomial: X ~ B(5000, 0.001).
Las características del tamaño de la muestra y la probabilidad relativamente baja que tiene, comprobaremos si podemos adaptar la distribución binomial a la de Poisson.
Para ello, debe cumplirse:
· n grande: n = 5000 OK.
· n·p = 5000·0.001 = 5 ≤ 7 OK.
Por lo tanto, se puede adaptar la variable aleatoria a la distribución de Poisson: X ~ P(5).
Debemos obtener la siguiente probabilidad:
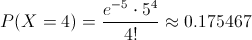
Por lo tanto, la probabilidad de que la compañía pague cuatro indemnizaciones en un determinado año es de, aproximadamente 0.175467.





2 comentarios:
Y si es a lo más 4 indemnizaciones?
se tomaria en cuenta el mismo trabajo que en distribucion binomial, sino que esta es poisson. Es decir que a 1 se le resta la P(3), P(2), P(1) y P(0)
Publicar un comentario