Ej31. Los datos siguientes son los sueldos mensuales y promedios de calificaciones para estudiantes que obtuvieron su licenciatura en administración:Calificación 2.6 3.4 3.6 3.2 3.5 2.9 Sueldo ($) 2800. .3100. .3500. .3000. .3400. .3100.
Obtener:
a) Encuentra la recta de regresión que relaciona ambas variables.
b) ¿Considera que hay relación lineal entre las variables?.
c) ¿Cuánto será el salario mensual de una persona cuya calificación promedio haya sido de 3,5 puntos?
Antes de empezar a resolver los apartados propuestos, hacemos una recopilación de datos que podemos extraer de la tabla dada, ya que posteriormente serán de gran utilidad.
· n = 6
· 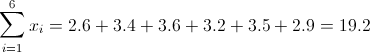
· 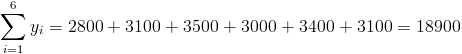
· 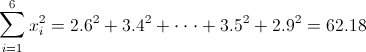
· 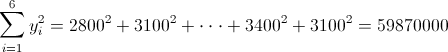
· 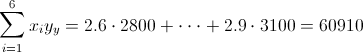
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.
Apartado a)
Para calcular la pendiente, la expresión matemática es:
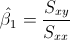
Para obtener su valor, necesitamos saber los valores de Sxy y Sxx:
·
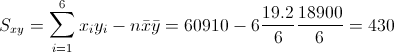
·
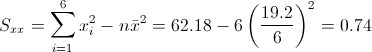
Por lo tanto, la pendiente es:
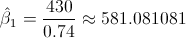
Una vez obtenida la pendiente, podemos tener el valor del estimador para la ordenada:
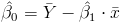
Sustituimos valores:
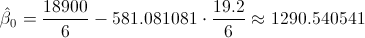
Por lo tanto, la ecuación de regresión ajustada es:
Apartado b)
Para saber si existen relación entre las variables, obtendremos el coeficiente de correlación, empleamos su expresión matemática:
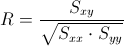
Debemos obtener el valor de Syy:
·
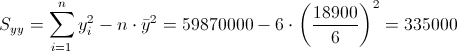
Sustituimos valores y obtenemos el resultado del coeficiente de determinación:
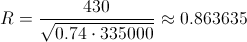
Por lo tanto, la relación entre las variables es de, aproximadamente 86.36%, al estar próximo a ±1 podemos determinar que existen evidencias significativas para decir qu existen relación entre ambas variables.
Apartado c)
En este apartado, debemos obtener el valor mediante la recta ajustada.
· Para Calificación = 3.5:
Por lo tanto, para una calificación promedio de 3.5 puntos se pronostica que su sueldo mensual, en dólares sea, aproximadamente de 3324.32





0 comentarios:
Publicar un comentario