Ej69. Dada la variable aleatoria X, cuya función de densidad es:
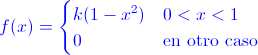
Hallar:
a) Determinar el valor de k para que f(x) sea una función de densidad legítima.
b) Obtener la la media y la varianza de la variable Y = 3X − 1.
Apartado a)
Empleamos la expresión de función de densidad de probabilidad:
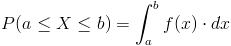
Para los intervalos expuestos en el enunciado del problema, en este caso:
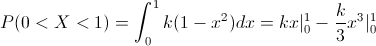
Sustituimos valores:
P(0 < .X< .1) = k(1 - 0) - (k/3)(1³) - 0³ = k - k/3 = (2/3)·k
Para que una variable aleatoria continua posea una función de densidad de probabilidad, tienen que cumplirse las siguientes condiciones:
1. f(x) > 0,...para todo x.
2.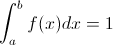
La función f(x) es mayor que cero, para ello, k debe ser mayor que cero, por lo que nos queda, satisfacer la segunda condición:
1. f(x) > 0,...para todo x.
2.
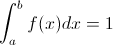
La función f(x) es mayor que cero, para ello, k debe ser mayor que cero, por lo que nos queda, satisfacer la segunda condición:
k = 3/2
Y así, obtenemos el valor de k y la solución de este apartado, para que f(x) sea una función de densidad de probabilidad, el valor de k es de 3/2.
Por lo tanto, la función de densidad de la variable aleatoria continua X queda:
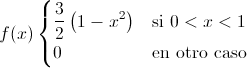
Apartado b)
En este apartado, debemos calcular la esperanza y la desviación estándar de la variable aleatoria continua, Y = 3X - 1.
Manipulamos la expresión de la variable continua Y:
· E[Y] = 3E[X] - E[1] = 3E[X] - 1
Para el cálculo de la esperanza, empleamos la siguiente expresión:
En este apartado, debemos calcular la esperanza y la desviación estándar de la variable aleatoria continua, Y = 3X - 1.
Manipulamos la expresión de la variable continua Y:
· E[Y] = 3E[X] - E[1] = 3E[X] - 1
Para el cálculo de la esperanza, empleamos la siguiente expresión:
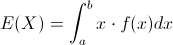
Por lo tanto, la esperanza de Y, será:
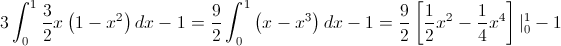
Y para la varianza, se empleará la siguiente expresión:
Var[X] = E(X²) - [E(X)]²Por lo tanto:
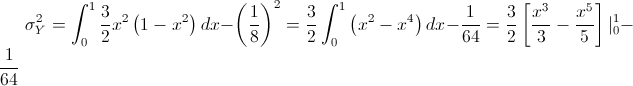
Sustituimos valores y obtenemos la varianza de la variable aleatoria continua Y:
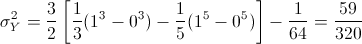

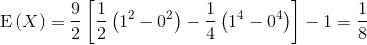




2 comentarios:
aqui un estudiante de ingenieria electronica industrial, estudiando mates 4 (estadistica), hay un error de calculo en el resultado de la media. el resultado seria 1/8. Gracias y estupenda pagina para hacer ejercicios de estadistica!!!
Buenas:
Muchas gracias por el dato, ya está subsanado, ha sido una errata puntual ya que al resolver la varianza se usa el valor correcto.
Me alegro que te sea de utilidad este blog.
Un saludo.
Publicar un comentario