Problema68: VAC

Ej68. Sea X una variable aleatoria con función de densidad uniforme en (-1, 1). Calcular la función de densidad de la variable Y = X².


Realizamos una recopilación de datos que nos ofrece el problema:

· La variable X se distribuye de forma uniforme: X ~ U(-1, 1)

La función de densidad de la distribución uniforme es:

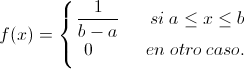
Sustituimos con los datos (el intervalo de acción) que nos ofrece el enunciado del problema:

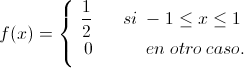
Bien, nos piden obtener la función de densidad de la variable Y, la cual se expresa de la siguiente forma:

· Y = X²

No es más que un cambio de variable, pero en fin, para obtener su función de densidad vamos previamente a obtener, su función de distribución acumulada. Para tal fin, aplicamos la definición:

· F(Y) = P(Y ≤ y)

Realizamos el cambio de variable:

· F(Y) = P(Y ≤ y) = P(X² ≤ y) = P(-√y ≤ x ≤ √y)

Sabemos que f(x) = 1/2, realizamos la integral desde -√y hasta √y para obtener la función de distribución acumulada:

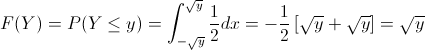
Pues bien, ya tenemos la función de distribución acumulada de Y:

· F(Y) = √y

Cuyo intervalo de acción es de 0 ≤ y ≤ 1 (No puede ir desde -1 hasta 1 ya que la raíz cuadrada de un número negativo no es válida).

Pues bien, simplemente nos queda deshacer el camino recorrido para obtener la función de densidad que nos piden en el enunciado del problema:

f(y) = F'(Y) = [y¹/²]' = (2√y)⁻¹

---

· NOTA: Este ejercicio se ha obtenido de los comentarios del capítulo: Variables Aleatorias Continuas.